Contents

HW 4

ISE-530 Homework IV: from Cottle-Thapa. Due Monday 11:59 PM October 12, 2020

  • Exercise 9.4, 9.20, 9.21, 9.22, and 10.5

  • Show that the univariate function \(f(x) = x^{4/3}\) has a unique minimizer at \(x = 0\) but that for any nonzero initial point, the Newton sequence for minimizing \(f\) diverges.

  • Compute the first two iterates of the Newton Method (with unit step) starting with \(x^0 = (0, 0)\) for minimizing the function: \(f(x_1, x_2) = 2x^4_1 + x^2_2 − 4x_1x_2 + 5x_2\). Do the same with the steepest descent method with exact line search.

  • Compute and solve the equation of the linear regression line corresponding to the univariate input-output data \((x, y)\) given by \(\{(−2, 12),(−1, 11),(0, 8),(1, 5),(2, 2),(3, −3)\}\). Plot these points and the computed line in the \((x, y)\)-plane.

  • Suppose that the (univariate) variable y is known to be a quadratic function of the variable \(x\); that is,

(216)\[\begin{align} y = ax^2 +bx + c, \end{align}\]

where the coefficients \(a, b, c\) are obtained by conducting an experiment in which values \(y_1, \cdots, y_n\) of the variable \(y\) are measured for corresponding values \(x_1, \cdots, x_n\) of the variable \(x\). Find the best least-squares fit of the quadratic polynomial using the data:

(217)\[\begin{align} &\{ (−2, −5),(−1, −1),(0, 4),(1, 7),(2, 6),(3, 5),(4, −1) \}. \end{align}\]

Plot these points and the computed quadratic curve in the \((x, y)\)-plane.

  • Show that the matrix

(218)\[\begin{align} \begin{bmatrix} x^4 & x^3 & x^2 \\ x^3 & x^2 & x \\ x^2 & x & 1 \\ \end{bmatrix} \end{align}\]

is positive semidefinite but not positive definite for all values of the scalar \(x\).

%load_ext autotime
%load_ext nb_black
%matplotlib inline

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

plt.rcParams["figure.dpi"] = 300
plt.rcParams["figure.figsize"] = (16, 12)

import pandas as pd
import numpy as np
import cvxpy as cp
import scipy as sp
from scipy import optimize
import functools

Chapter 9

9.4

Apply, in turn, the Bisection Method, Newton’s Method, the Secant Method, and the Regula Falsi Method to find a zero of the polynomial \(g(x) = x^3 − 7x^2 + 10x − 6\) over the interval \([2, 6]\).

g = lambda x: x ** 3 - 7 * x ** 2 + 10 * x - 6
g_prime = lambda x: 3 * (x ** 2) - 14 * x + 10  # Derivative of g
quadratic_formula = lambda a, b, c: (
    (-b + (b ** 2 - 4 * a * c) ** 0.5) / (2 * a),
    (-b - (b ** 2 - 4 * a * c) ** 0.5) / (2 * a),
)

time: 1.26 ms

Bisection Method

def bisection_root_finding(f, interval=[2, 6], δ=1e-05):
    assert (len(interval) == 2) & (
        interval[1] > interval[0]
    ), "interval must only have 2 values and b > a."
    root_candidate = np.mean(interval)
    while True:
        # 1. If |b−a| ≤ δ or f(c)=0, stop and report the zero as x∗=c.
        if np.allclose(np.abs(interval[1] - interval[0]), 0, rtol=δ) or np.allclose(
            f(root_candidate), 0, rtol=1e-5
        ):
            return root_candidate

        # 2. If f(a)f(c)>0, let a←c else let b←c to create a new interval.
        print(
            f"x = ({np.round(interval, 5)}/2) = {np.round(root_candidate, 5)}",
            f"g(x) = {np.round(f(root_candidate), 5)}",
        )
        if np.prod(np.sign([f(root_candidate), f(interval[1])])) < 0:
            interval = [root_candidate, interval[1]]
        else:
            interval = [interval[0], root_candidate]

        # 3. Find the midpoint c of the new interval and evaluate f(c).
        root_candidate = np.mean(interval)

    return root_candidate

time: 2.25 ms

bisection_root_finding(f=g, interval=[2, 6])

x = ([2 6]/2) = 4.0 g(x) = -14.0
x = ([4. 6.]/2) = 5.0 g(x) = -6.0
x = ([5. 6.]/2) = 5.5 g(x) = 3.625
x = ([5.  5.5]/2) = 5.25 g(x) = -1.73438
x = ([5.25 5.5 ]/2) = 5.375 g(x) = 0.80273
x = ([5.25  5.375]/2) = 5.3125 g(x) = -0.50073
x = ([5.3125 5.375 ]/2) = 5.34375 g(x) = 0.14218
x = ([5.3125  5.34375]/2) = 5.32812 g(x) = -0.18147
x = ([5.32812 5.34375]/2) = 5.33594 g(x) = -0.02019
x = ([5.33594 5.34375]/2) = 5.33984 g(x) = 0.06086
x = ([5.33594 5.33984]/2) = 5.33789 g(x) = 0.0203
x = ([5.33594 5.33789]/2) = 5.33691 g(x) = 4e-05
x = ([5.33594 5.33691]/2) = 5.33643 g(x) = -0.01008
x = ([5.33643 5.33691]/2) = 5.33667 g(x) = -0.00502
x = ([5.33667 5.33691]/2) = 5.33679 g(x) = -0.00249
x = ([5.33679 5.33691]/2) = 5.33685 g(x) = -0.00122
x = ([5.33685 5.33691]/2) = 5.33688 g(x) = -0.00059
x = ([5.33688 5.33691]/2) = 5.3369 g(x) = -0.00027
x = ([5.3369  5.33691]/2) = 5.33691 g(x) = -0.00012
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = -4e-05
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = 0.0
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = -2e-05
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = -1e-05
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = -0.0
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = 0.0
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = -0.0
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = 0.0
x = ([5.33691 5.33691]/2) = 5.33691 g(x) = 0.0

5.3369119837880135

time: 14.4 ms

Newton’s Method

def newton_raphson_root_finding(f, f_prime, x_0, δ=1e-05):
    x_k = x_0  # x_k
    while True:
        print(f"New root candidate: {x_k}")
        # 1. If |f(xk)| ≤ δ, stop and report a zero of f as x∗ = xk.
        if np.allclose(f(x_k), 0, rtol=δ):
            return x_k

        # 2. Determine pk = −f(xk)/f′(xk)
        p_k = -f(x_k) / f_prime(x_k)

        # 3. Set the steplength αk = 1.
        α_k = 1

        # 4. Let xk+1 = xk + αkpk = xk − f(xk)/f′(xk), and compute f(xk+1).
        x_k += α_k * p_k

        # 5. Let k←k+1 and return to Step 1.

    return x_k

time: 1.18 ms

newton_raphson_root_finding(f=g, f_prime=g_prime, x_0=6)

New root candidate: 6
New root candidate: 5.470588235294118
New root candidate: 5.3440601662117935
New root candidate: 5.336934090072915
New root candidate: 5.336911983591771

5.336911983591771

time: 3.14 ms

Secant Method

def secant_root_finding(f, x_0, x_1, δ=1e-05):
    x_k, x_k_1 = x_1, x_0  # x_k, x_k-1
    while True:
        print(f"New root candidate: {x_k}")
        # 1. If |f(xk)| ≤ δ, stop and report a zero of f as x∗ = xk.
        if np.allclose(f(x_k), 0, rtol=δ):
            return x_k

        # 2. Determine pk = −f(xk) [(xk − xk−1) / (f(xk) − f(xk−1))].
        p_k = -f(x_k) * ((x_k - x_k_1) / (f(x_k) - f(x_k_1)))

        # 3. Set the steplength αk = 1.
        α_k = 1

        # 4. Let xk+1 = xk +αkpk = xk −f(xk) [(xk − xk−1) / (f(xk) − f(xk−1))], and compute f(xk+1).
        x_k_1 = x_k
        x_k += α_k * p_k

        # 5. Let k←k+1 and return to Step 1.

    return x_k

time: 1.48 ms

secant_root_finding(f=g, x_0=8, x_1=7)

New root candidate: 7
New root candidate: 6.135135135135135
New root candidate: 5.656587804167496
New root candidate: 5.418190380860478
New root candidate: 5.346901914851419
New root candidate: 5.337254755192322
New root candidate: 5.3369134667667195
New root candidate: 5.336911983600337

5.336911983600337

time: 3.31 ms

Regula Falsi Method

def regula_falsi_root_finding(f, x_0, x_1, δ=1e-05):
    assert (
        f(x_0) * f(x_1) < 0
    ), "f(x_0)f(x_1) < 0, choose another pair of values for x_0 and x_1."
    x_k, x_k_1 = x_1, x_0  # x_k, x_k-1
    while True:
        print(f"New root candidate: {x_k}")
        # 1. If |f(xk)| ≤ δ, stop and report a zero of f as x∗ = xk.
        if np.allclose(f(x_k), 0, rtol=δ):
            return x_k

        # 2. Determine pk = −f(xk) [(xk − xk−1) / (f(xk) − f(xk−1))].
        p_k = -f(x_k) * ((x_k - x_k_1) / (f(x_k) - f(x_k_1)))

        # 3. Set the steplength αk = 1.
        α_k = 1

        # 5. If f(xk+1)f(xk−1) < 0, set xk = xk−1.
        if f(x_k + α_k * p_k) * f(x_k_1) < 0:
            x_k_1 = x_k

        # 4. Let xk+1 = xk +αkpk = xk −f(xk) [(xk − xk−1) / (f(xk) − f(xk−1))], and compute f(xk+1).
        x_k += α_k * p_k

        # 6. Let k←k+1 and return to Step 1.

    return x_k

time: 1.7 ms

regula_falsi_root_finding(f=g, x_0=5, x_1=7)

New root candidate: 7
New root candidate: 5.171428571428572
New root candidate: 5.365835448708374
New root candidate: 5.334736464207193
New root candidate: 5.337077382052705
New root candidate: 5.336911826879108
New root candidate: 5.3369119835274486

5.3369119835274486

time: 3.03 ms

x = np.linspace(2, 6, int(1e3))
plt.plot(x, g(x), label="$g(x)$")
plt.plot(x, np.zeros(x.shape))
plt.scatter(5.34, 0, c="r", marker="x", s=100, label="root = (5.34, 0)")
plt.ylabel("$g(x)$")
plt.xlabel("$x$")
plt.legend()
plt.grid(True)
plt.show()
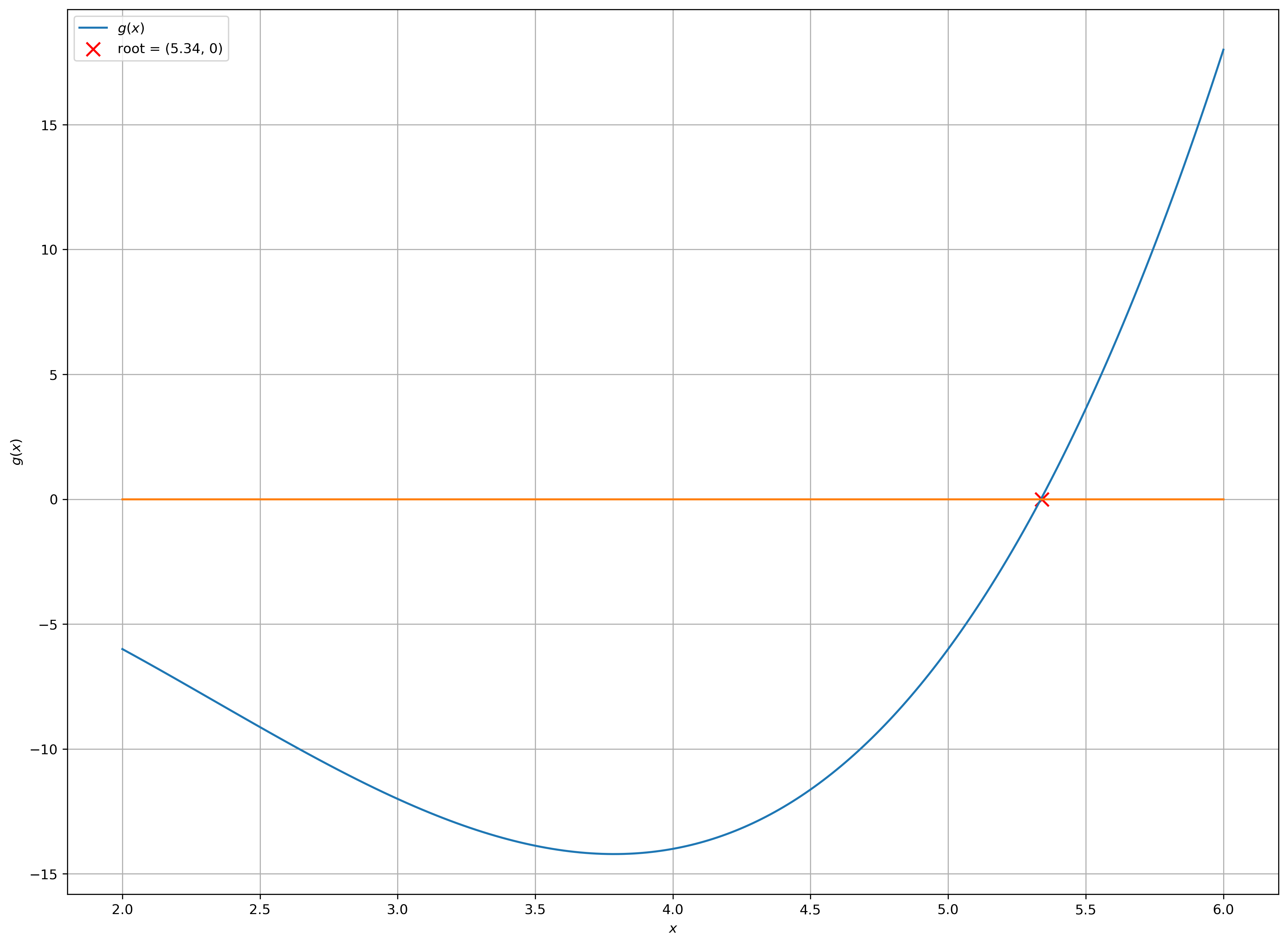
../../_images/hw4_17_0.png 
time: 1.92 s

9.20

Consider the function

(219)\[\begin{align} f(x_1, x_2) &= ax^2_1 + bx^2_2 + cx_1 + dx_2, \end{align}\]

with \(a > 0\) and \(b < 0\).

(a) Show that \(f(x_1, x_2)\) has only one stationary point.

Gradient Vector:

(220)\[\begin{align} g(x_1, x_2) &= \begin{bmatrix} 2ax_1 + c \\ 2bx_2 + d \end{bmatrix} \\ \end{align}\]

First-order Stationarity condition:

(221)\[\begin{align} g(x_1, x_2) &= 0 \\ \begin{bmatrix} 2ax_1 + c \\ 2bx_2 + d \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix} \\ \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} &= \begin{bmatrix} -\frac{c}{2a} \\ -\frac{d}{2b} \\ \end{bmatrix} \\ \end{align}\]

Hence, for fixed constants \(a, b, c, d\), there is only one stationary point given by the formula above. \(\blacksquare\)

(b) Show that this stationary point is neither a minimizer nor maximizer for \(f\).

Hessian Matrix:

(222)\[\begin{align} G(x) &= \begin{bmatrix} 2a & 0 \\ 0 & 2b \\ \end{bmatrix} \\ \end{align}\]

As observed, since \(a > 0, b < 0\), the Hessian has 1 positive eigenvalue \(2a\), and 1 negative eigenvalue \(2b\), meaning that it is neither positive semi-definite (all eigenvalues >= 0), nor positive definite (all eigenvalues > 0), nor negative definite (all eigenvalues < 0), nor negative semi-definite (all eigenvalues <= 0), and is classified as indefinite and is a saddle point, neither a minimizer or maximizer for \(f\). \(\blacksquare\)

(c) With \(a=1,b=−3,c=3,d=6\),draw a few contour lines of \(f\).

f = (
    lambda x, a=1, b=-3, c=3, d=6: a * (x[0] ** 2)
    + b * (x[1] ** 2)
    + c * x[0]
    + d * x[1]
)

x_1, x_2 = np.linspace(-5, 5, 1000), np.linspace(-5, 5, 1000)
X, Y = np.meshgrid(x_1, x_2)
Z = f(x=[X, Y])
ax = plt.axes(projection="3d")
ax.view_init(20, 40)
ax.contour3D(X, Y, Z, 200, cmap="binary")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$f(x_1, x_2)$")
plt.title("$f(x_1, x_2) = x^2_1 -3x^2_2 + 3x_1 + 6x_2$")
plt.show()
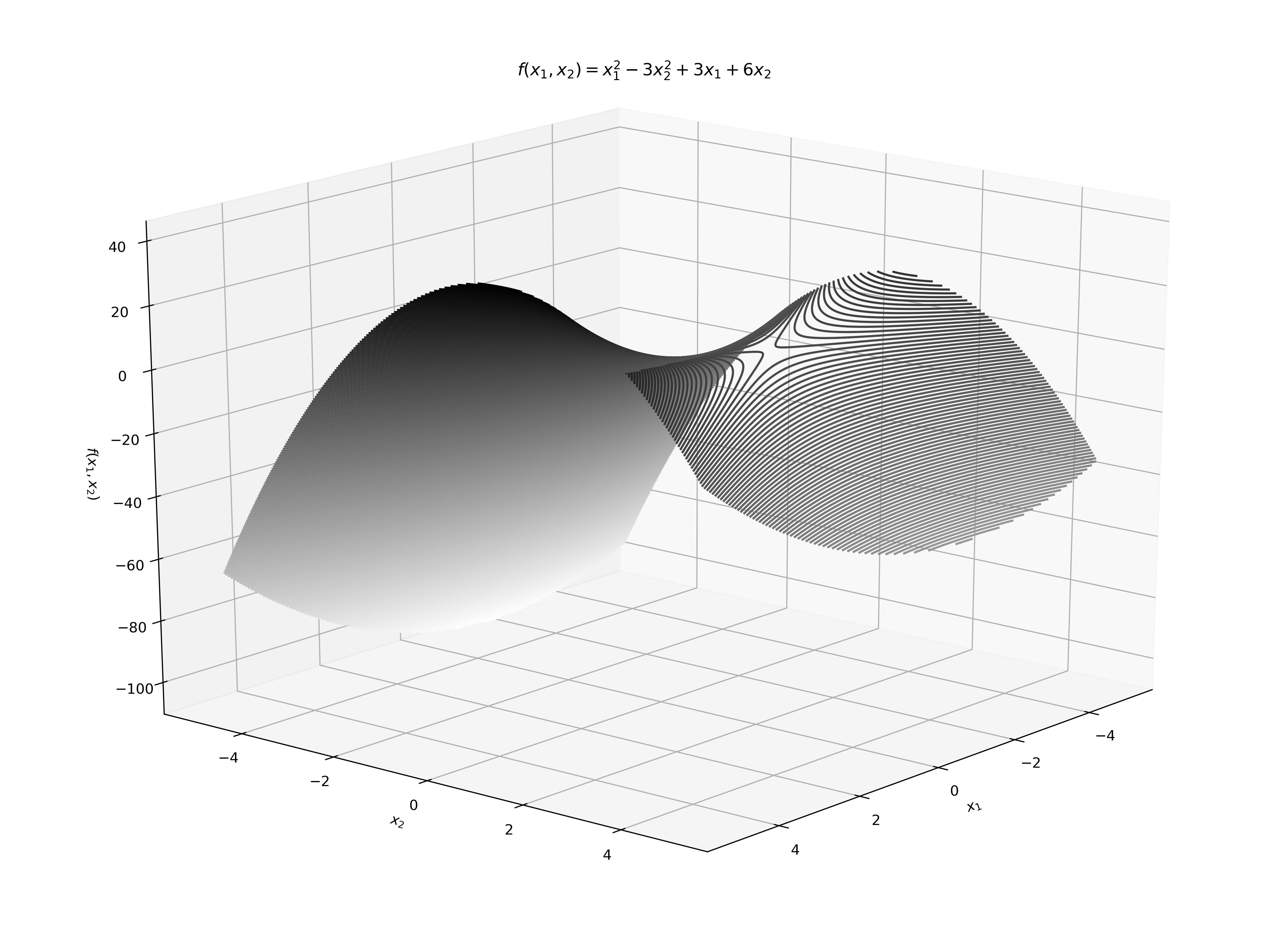
../../_images/hw4_27_0.png 
time: 6.08 s

9.21

(Based on Exercise 4 in Fletcher [68, p. 30].) The function \(f(x_1, x_2) = x^5_1 +(x^2_1 − x_2)^2\) has only one stationary point (i.e., solution of \(\nabla f(x_1, x_2) = 0\)). Find it and show that it is neither a local maximizer nor a local minimizer.

Gradient Vector:

(223)\[\begin{align} \nabla f(x_1, x_2) &= \begin{bmatrix} 5x^4_1 + 4x^3_1 - 4x_1x_2 \\ -2x^2_1 + 2x_2 \\ \end{bmatrix} \\ \end{align}\]

First-order Stationarity condition:

(224)\[\begin{align} \nabla f(x_1, x_2) &= 0 \\ \begin{bmatrix} 5x^4_1 + 4x^3_1 - 4x_1x_2 \\ -2x^2_1 + 2x_2 \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix} \\ \text{Let }x_2 = x^2_1, \\ \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix} \\ \end{align}\]

Hessian Matrix:

(225)\[\begin{align} \nabla^2 f(x_1, x_2) &= \begin{bmatrix} 20x^3_1 + 12x^2_1 -4x_2 & -4x_1 \\ -4x_1 & 2 \\ \end{bmatrix} \\ \end{align}\]

At the stationary point:

(226)\[\begin{align} \nabla^2 f(x_1, x_2) &= \begin{bmatrix} 0 & 0 \\ 0 & 2 \\ \end{bmatrix} \\ \end{align}\]

We have a positive semi-definite Hessian, which although satisfies the second order necessary conditions for optimality, it does not the sufficiency conditions for optimality (Hessian needs to be positive definite, not just positive semi-definite), which does means it is not a local minimizer.

However, at the stationary point, \(f(x_1=0, x_2=0) = 0\) and \(f(x_1>0, x_2>0) > 0\) while \(f(x_1<0, x_2<0) < 0\), meaning that it is neither a local minimizer or maximizer at the stationary point. \(\blacksquare\)

Coercivity: We also see that \(x^5_1\) term dominates in \(f\) at the extreme points of the function. As (\(x_1 \rightarrow \infty / -\infty\) and \(x_2 \rightarrow \infty / -\infty\)), \(x^5_1\) term dominates and if \(x_1 \rightarrow \infty\), \(f \rightarrow \infty\) and if \(x_1 \rightarrow -\infty\), \(f \rightarrow -\infty\).

f = lambda x: x[0] ** 5 + (x[0] ** 2 - x[1]) ** 2

x_1, x_2 = np.linspace(-5, 5, 1000), np.linspace(-5, 5, 1000)
X, Y = np.meshgrid(x_1, x_2)
Z = f(x=[X, Y])
ax = plt.axes(projection="3d")
ax.view_init(5, 70)
ax.contour3D(X, Y, Z, 200, cmap="binary")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$f(x_1, x_2)$")
plt.title("$f(x_1, x_2) = x^5_1 +(x^2_1 − x_2)^2$")
plt.show()
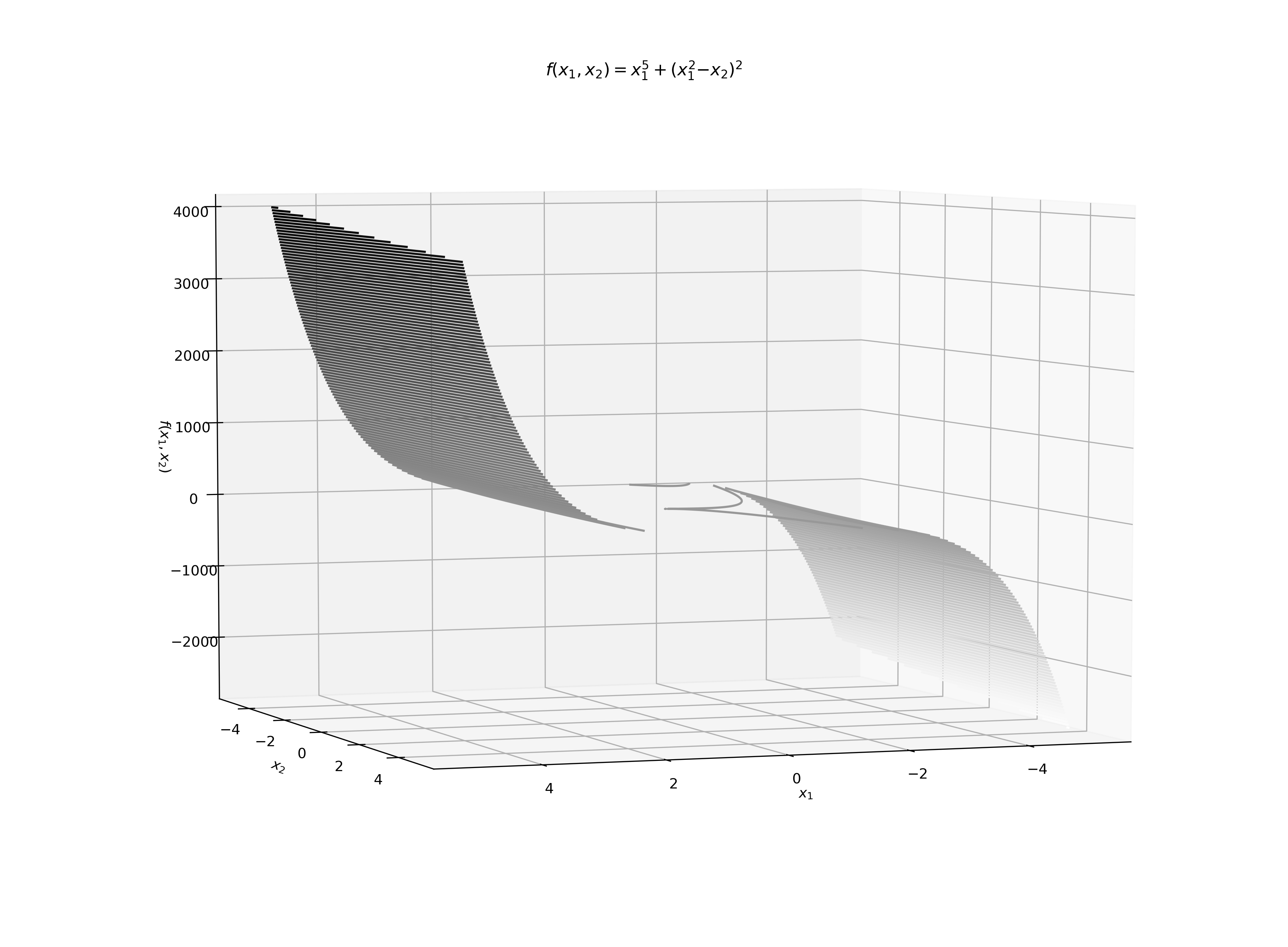
../../_images/hw4_36_0.png 
time: 5.31 s

9.22

Find a global minimum of the function

(227)\[\begin{align} f(x_1,x_2,x_3) &= 6x^2_1 + 4x^2_2 + 2x^2_3 + 2x_1x_2 + 2x_1x_3 + 2x_2x_3 − 11x_1 − 12x_2 − 9x_3. \end{align}\]

Gradient Vector:

(228)\[\begin{align} \nabla f(x_1, x_2, x_3) &= \begin{bmatrix} 12x_1 + 2x_2 + 2x_3 -11 \\ 8x_2 + 2x_1 + 2x_3 - 12 \\ 4x_3 + 2x_1 + 2x_2 - 9 \\ \end{bmatrix} \\ \end{align}\]

First-order Stationarity condition:

(229)\[\begin{align} \nabla f(x_1, x_2, x_3) &= 0 \\ \begin{bmatrix} 12x_1 + 2x_2 + 2x_3 -11 \\ 8x_2 + 2x_1 + 2x_3 - 12 \\ 4x_3 + 2x_1 + 2x_2 - 9 \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix} \\ \begin{bmatrix} 12 & 2 & 2 \\ 2 & 8 & 2 \\ 2 & 2 & 4 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} &= \begin{bmatrix} 11 \\ 12 \\ 9 \\ \end{bmatrix} \\ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} &= \begin{bmatrix} 12 & 2 & 2 \\ 2 & 8 & 2 \\ 2 & 2 & 4 \\ \end{bmatrix}^{-1} \begin{bmatrix} 11 \\ 12 \\ 9 \\ \end{bmatrix} \\ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} &= \begin{bmatrix} 0.5 \\ 1 \\ 1.5 \\ \end{bmatrix} \end{align}\]

Hessian Matrix:

(230)\[\begin{align} \nabla^2 f(x_1, x_2, x_3) &= \begin{bmatrix} 12 & 2 & 2 \\ 2 & 8 & 2 \\ 2 & 2 & 4 \\ \end{bmatrix} \\ \end{align}\]
np.linalg.eigvals(np.array([[12, 2, 2], [2, 8, 2], [2, 2, 4]]))

array([13.55691424,  7.42166291,  3.02142286])

time: 3.95 ms

Since all the eigenvalues \(\lambda\) of the Hessian matrix are positive, regardless of which point \(x_1, x_2, x_3\), we have a positive definite Hessian and hence, strictly convex with 1 global minimum (ordinarily, if the Hessian is just positive definite at that point thenit’ll just be a strict local minimizer), which is the single stationary point we found.

f = (
    lambda x: 6 * (x[0] ** 2)
    + 4 * (x[1] ** 2)
    + 2 * (x[2] ** 2)
    + 2 * x[0] * x[1]
    + 2 * x[0] * x[2]
    + 2 * x[1] * x[2]
    - 11 * x[0]
    - 12 * x[1]
    - 9 * x[2]
)

optimize.minimize(fun=f, x0=np.zeros((3,)))

      fun: -15.499999999996737
 hess_inv: array([[ 0.0921055 , -0.01317824, -0.03944193],
       [-0.01317824,  0.14513135, -0.06639581],
       [-0.03944193, -0.06639581,  0.30356681]])
      jac: array([ 1.43051147e-06, -3.81469727e-06,  3.09944153e-06])
  message: 'Optimization terminated successfully.'
     nfev: 40
      nit: 8
     njev: 10
   status: 0
  success: True
        x: array([0.50000005, 0.99999923, 1.50000113])

time: 8.72 ms

Global minimum: -15.5

Chapter 10

10.5

Define the function

(231)\[\begin{align} f_c(x) &= cx^2_1 + x^2_2. \end{align}\]
f = lambda x, c: c * x[0] ** 2 + x[1] ** 2
f_prime = lambda x, c: np.array([2 * c * x[0], 2 * x[1]])
hessian = lambda x, c: np.array([[2 * c, 0], [0, 2]])
c_vals = [2, 10, 100]

x_1, x_2 = np.linspace(-5, 5, 1000), np.linspace(-5, 5, 1000)
X, Y = np.meshgrid(x_1, x_2)
Z = {c: f(x=[X, Y], c=c) for c in c_vals}
ax = plt.axes(projection="3d")
ax.view_init(20, 50)
for c, cmap in zip(c_vals, ["Blues", "Greens", "Oranges"]):
    ax.contour3D(X, Y, Z[c], 200, cmap=cmap, label=f"$f_{c}(x) = {c}x^2_1 + x^2_2$")
ax.legend()
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$f_c(x)$")
plt.title("$f_c(x) = cx^2_1 + x^2_2$")
plt.show()

/opt/anaconda3/envs/ml/lib/python3.7/site-packages/ipykernel_launcher.py:12: UserWarning: The following kwargs were not used by contour: 'label'
  if sys.path[0] == '':
No handles with labels found to put in legend.
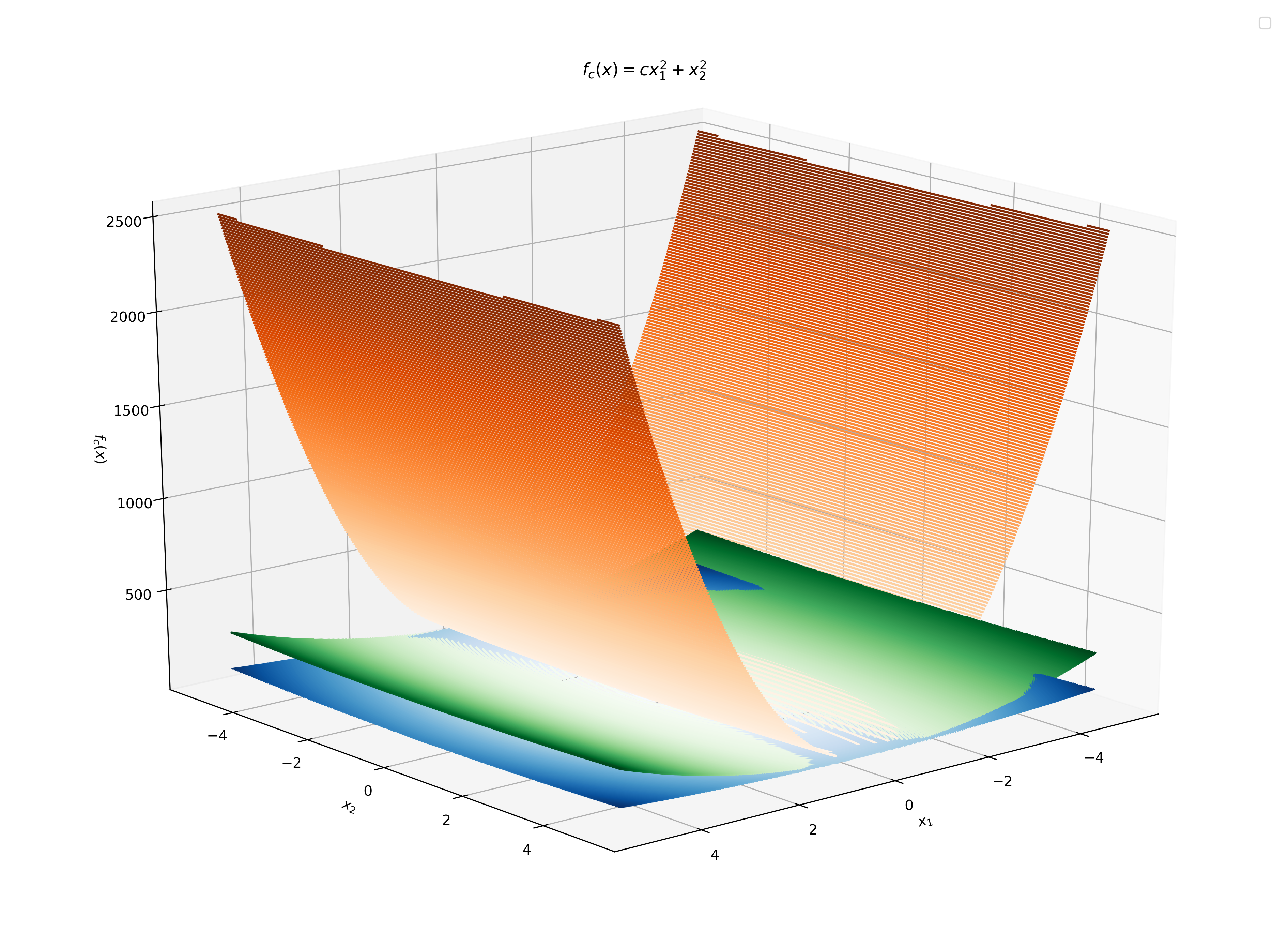
../../_images/hw4_47_1.png 
time: 17 s

(a) Starting with the point \(x = (10, 10)^\top\) , carry out three iterations of the Steepest-descent Method to minimize \(f_c(x)\) when \(c = 2, c = 10,\) and \(c = 100\).

def simple_steplength(f, f_prime, x_k, p_k, μ=1e-4):
    # 1. Set α=1.
    α = 1
    while True:
        # 2. If f(xk+αpk) ≤ f(xk)+μαgkpk, set αk=α and stop.
        if f(x_k + α * p_k) <= f(x_k) + μ * α * f_prime(x_k).T @ p_k:
            return α
        else:
            # 3. Set α=α/2 and go to Step2.
            α /= 2


def steepest_descent(f, f_prime, x_0, ε=1e-15, steplength_algo=simple_steplength):
    k, x_k = 0, x_0
    while True:

        # 1. Test for Convergence
        if np.allclose(f_prime(x_k), 0, rtol=ε):
            return x_k

        # 2. Compute a search direction
        p_k = -f_prime(x_k)

        # 3. Compute a steplength
        α_k = steplength_algo(f=f, f_prime=f_prime, x_k=x_k, p_k=p_k, μ=1e-4)

        print(
            f"Iteration: {k} - x_{k} = {np.round(x_k, 5)}, p_k = {np.round(p_k, 5)}, α_k = {np.round(α_k, 5)}"
        )

        # 4. Update the iterate and return to Step 1
        k += 1
        x_k += α_k * p_k

        # Check for divergence
        if np.allclose(x_k, x_k + α_k * p_k) and k > 1:
            print("Series diverged.")
            break

time: 2.47 ms

c = 2
print(f"Steepest Descent with c={c}:")
print("=" * 30)
steepest_descent(
    f=functools.partial(f, c=c),
    f_prime=functools.partial(f_prime, c=c),
    x_0=np.array([10.0, 10.0]),
    ε=1e-15,
)

Steepest Descent with c=2:
==============================
Iteration: 0 - x_0 = [10. 10.], p_k = [-40. -20.], α_k = 0.5
Iteration: 1 - x_1 = [-10.   0.], p_k = [40. -0.], α_k = 0.25

array([0., 0.])

time: 4.93 ms

c = 10
print(f"Steepest Descent with c={c}:")
print("=" * 30)
steepest_descent(
    f=functools.partial(f, c=c),
    f_prime=functools.partial(f_prime, c=c),
    x_0=np.array([10.0, 10.0]),
    ε=1e-15,
)

Steepest Descent with c=10:
==============================
Iteration: 0 - x_0 = [10. 10.], p_k = [-200.  -20.], α_k = 0.0625
Iteration: 1 - x_1 = [-2.5   8.75], p_k = [ 50.  -17.5], α_k = 0.0625
Iteration: 2 - x_2 = [0.625   7.65625], p_k = [-12.5    -15.3125], α_k = 0.125
Iteration: 3 - x_3 = [-0.9375   5.74219], p_k = [ 18.75    -11.48438], α_k = 0.125
Iteration: 4 - x_4 = [1.40625 4.30664], p_k = [-28.125    -8.61328], α_k = 0.0625
Iteration: 5 - x_5 = [-0.35156  3.76831], p_k = [ 7.03125 -7.53662], α_k = 0.125
Iteration: 6 - x_6 = [0.52734 2.82623], p_k = [-10.54688  -5.65247], α_k = 0.125
Iteration: 7 - x_7 = [-0.79102  2.11967], p_k = [15.82031 -4.23935], α_k = 0.0625
Iteration: 8 - x_8 = [0.19775 1.85472], p_k = [-3.95508 -3.70943], α_k = 0.125
Iteration: 9 - x_9 = [-0.29663  1.39104], p_k = [ 5.93262 -2.78207], α_k = 0.0625
Iteration: 10 - x_10 = [0.07416 1.21716], p_k = [-1.48315 -2.43431], α_k = 0.25
Iteration: 11 - x_11 = [-0.29663  0.60858], p_k = [ 5.93262 -1.21716], α_k = 0.0625
Iteration: 12 - x_12 = [0.07416 0.53251], p_k = [-1.48315 -1.06501], α_k = 0.125
Iteration: 13 - x_13 = [-0.11124  0.39938], p_k = [ 2.22473 -0.79876], α_k = 0.0625
Iteration: 14 - x_14 = [0.02781 0.34946], p_k = [-0.55618 -0.69891], α_k = 0.125
Iteration: 15 - x_15 = [-0.04171  0.26209], p_k = [ 0.83427 -0.52419], α_k = 0.125
Iteration: 16 - x_16 = [0.06257 0.19657], p_k = [-1.25141 -0.39314], α_k = 0.0625
Iteration: 17 - x_17 = [-0.01564  0.172  ], p_k = [ 0.31285 -0.344  ], α_k = 0.125
Iteration: 18 - x_18 = [0.02346 0.129  ], p_k = [-0.46928 -0.258  ], α_k = 0.125
Iteration: 19 - x_19 = [-0.0352   0.09675], p_k = [ 0.70392 -0.1935 ], α_k = 0.0625
Iteration: 20 - x_20 = [0.0088  0.08466], p_k = [-0.17598 -0.16931], α_k = 0.125
Iteration: 21 - x_21 = [-0.0132   0.06349], p_k = [ 0.26397 -0.12698], α_k = 0.0625
Iteration: 22 - x_22 = [0.0033  0.05556], p_k = [-0.06599 -0.11111], α_k = 0.25
Iteration: 23 - x_23 = [-0.0132   0.02778], p_k = [ 0.26397 -0.05556], α_k = 0.0625
Iteration: 24 - x_24 = [0.0033  0.02431], p_k = [-0.06599 -0.04861], α_k = 0.125
Iteration: 25 - x_25 = [-0.00495  0.01823], p_k = [ 0.09899 -0.03646], α_k = 0.0625
Iteration: 26 - x_26 = [0.00124 0.01595], p_k = [-0.02475 -0.0319 ], α_k = 0.125
Iteration: 27 - x_27 = [-0.00186  0.01196], p_k = [ 0.03712 -0.02393], α_k = 0.125
Iteration: 28 - x_28 = [0.00278 0.00897], p_k = [-0.05568 -0.01794], α_k = 0.0625
Iteration: 29 - x_29 = [-0.0007   0.00785], p_k = [ 0.01392 -0.0157 ], α_k = 0.125
Iteration: 30 - x_30 = [0.00104 0.00589], p_k = [-0.02088 -0.01178], α_k = 0.125
Iteration: 31 - x_31 = [-0.00157  0.00442], p_k = [ 0.03132 -0.00883], α_k = 0.0625
Iteration: 32 - x_32 = [0.00039 0.00386], p_k = [-0.00783 -0.00773], α_k = 0.125
Iteration: 33 - x_33 = [-0.00059  0.0029 ], p_k = [ 0.01175 -0.0058 ], α_k = 0.0625
Iteration: 34 - x_34 = [0.00015 0.00254], p_k = [-0.00294 -0.00507], α_k = 0.25
Iteration: 35 - x_35 = [-0.00059  0.00127], p_k = [ 0.01175 -0.00254], α_k = 0.0625
Iteration: 36 - x_36 = [0.00015 0.00111], p_k = [-0.00294 -0.00222], α_k = 0.125
Iteration: 37 - x_37 = [-0.00022  0.00083], p_k = [ 0.0044  -0.00166], α_k = 0.0625
Iteration: 38 - x_38 = [6.0e-05 7.3e-04], p_k = [-0.0011  -0.00146], α_k = 0.125
Iteration: 39 - x_39 = [-8.0e-05  5.5e-04], p_k = [ 0.00165 -0.00109], α_k = 0.125
Iteration: 40 - x_40 = [0.00012 0.00041], p_k = [-0.00248 -0.00082], α_k = 0.0625
Iteration: 41 - x_41 = [-3.0e-05  3.6e-04], p_k = [ 0.00062 -0.00072], α_k = 0.125
Iteration: 42 - x_42 = [5.0e-05 2.7e-04], p_k = [-0.00093 -0.00054], α_k = 0.125
Iteration: 43 - x_43 = [-7.e-05  2.e-04], p_k = [ 0.00139 -0.0004 ], α_k = 0.0625
Iteration: 44 - x_44 = [2.0e-05 1.8e-04], p_k = [-0.00035 -0.00035], α_k = 0.125
Iteration: 45 - x_45 = [-3.0e-05  1.3e-04], p_k = [ 0.00052 -0.00026], α_k = 0.0625
Iteration: 46 - x_46 = [1.0e-05 1.2e-04], p_k = [-0.00013 -0.00023], α_k = 0.25
Iteration: 47 - x_47 = [-3.e-05  6.e-05], p_k = [ 0.00052 -0.00012], α_k = 0.0625
Iteration: 48 - x_48 = [1.e-05 5.e-05], p_k = [-0.00013 -0.0001 ], α_k = 0.125
Iteration: 49 - x_49 = [-1.e-05  4.e-05], p_k = [ 2.e-04 -8.e-05], α_k = 0.0625
Iteration: 50 - x_50 = [0.e+00 3.e-05], p_k = [-5.e-05 -7.e-05], α_k = 0.125
Iteration: 51 - x_51 = [-0.e+00  2.e-05], p_k = [ 7.e-05 -5.e-05], α_k = 0.125
Iteration: 52 - x_52 = [1.e-05 2.e-05], p_k = [-1.1e-04 -4.0e-05], α_k = 0.0625
Iteration: 53 - x_53 = [-0.e+00  2.e-05], p_k = [ 3.e-05 -3.e-05], α_k = 0.125
Iteration: 54 - x_54 = [0.e+00 1.e-05], p_k = [-4.e-05 -2.e-05], α_k = 0.125
Iteration: 55 - x_55 = [-0.e+00  1.e-05], p_k = [ 6.e-05 -2.e-05], α_k = 0.0625
Iteration: 56 - x_56 = [0.e+00 1.e-05], p_k = [-2.e-05 -2.e-05], α_k = 0.125
Iteration: 57 - x_57 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -1.e-05], α_k = 0.0625
Iteration: 58 - x_58 = [0.e+00 1.e-05], p_k = [-1.e-05 -1.e-05], α_k = 0.25
Iteration: 59 - x_59 = [-0.  0.], p_k = [ 2.e-05 -1.e-05], α_k = 0.0625
Iteration: 60 - x_60 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.125
Iteration: 61 - x_61 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.0625
Iteration: 62 - x_62 = [0. 0.], p_k = [-0. -0.], α_k = 0.125
Iteration: 63 - x_63 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.125
Iteration: 64 - x_64 = [0. 0.], p_k = [-0. -0.], α_k = 0.0625
Iteration: 65 - x_65 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.125
Iteration: 66 - x_66 = [0. 0.], p_k = [-0. -0.], α_k = 0.125
Iteration: 67 - x_67 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.0625
Iteration: 68 - x_68 = [0. 0.], p_k = [-0. -0.], α_k = 0.125
Iteration: 69 - x_69 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.0625
Iteration: 70 - x_70 = [0. 0.], p_k = [-0. -0.], α_k = 0.25
Iteration: 71 - x_71 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.0625
Iteration: 72 - x_72 = [0. 0.], p_k = [-0. -0.], α_k = 0.125
Iteration: 73 - x_73 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.0625
Iteration: 74 - x_74 = [0. 0.], p_k = [-0. -0.], α_k = 0.25
Iteration: 75 - x_75 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.0625
Iteration: 76 - x_76 = [0. 0.], p_k = [-0. -0.], α_k = 0.125
Iteration: 77 - x_77 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.0625
Series diverged.
time: 43.6 ms

c = 100
print(f"Steepest Descent with c={c}:")
print("=" * 30)
steepest_descent(
    f=functools.partial(f, c=c),
    f_prime=functools.partial(f_prime, c=c),
    x_0=np.array([10.0, 10.0]),
    ε=1e-15,
)

Steepest Descent with c=100:
==============================
Iteration: 0 - x_0 = [10. 10.], p_k = [-2000.   -20.], α_k = 0.00781
Iteration: 1 - x_1 = [-5.625    9.84375], p_k = [1125.      -19.6875], α_k = 0.00781
Iteration: 2 - x_2 = [3.16406 9.68994], p_k = [-632.8125   -19.37988], α_k = 0.00781
Iteration: 3 - x_3 = [-1.77979  9.53854], p_k = [355.95703 -19.07707], α_k = 0.00781
Iteration: 4 - x_4 = [1.00113 9.3895 ], p_k = [-200.22583  -18.77899], α_k = 0.00781
Iteration: 5 - x_5 = [-0.56314  9.24279], p_k = [112.62703 -18.48557], α_k = 0.00781
Iteration: 6 - x_6 = [0.31676 9.09837], p_k = [-63.3527  -18.19673], α_k = 0.00781
Iteration: 7 - x_7 = [-0.17818  8.95621], p_k = [ 35.6359  -17.91241], α_k = 0.00781
Iteration: 8 - x_8 = [0.10023 8.81626], p_k = [-20.04519 -17.63253], α_k = 0.01562
Iteration: 9 - x_9 = [-0.21298  8.54076], p_k = [ 42.59603 -17.08151], α_k = 0.00781
Iteration: 10 - x_10 = [0.1198  8.40731], p_k = [-23.96027 -16.81461], α_k = 0.00781
Iteration: 11 - x_11 = [-0.06739  8.27594], p_k = [ 13.47765 -16.55189], α_k = 0.01562
Iteration: 12 - x_12 = [0.1432  8.01732], p_k = [-28.64001 -16.03464], α_k = 0.00781
Iteration: 13 - x_13 = [-0.08055  7.89205], p_k = [ 16.11   -15.7841], α_k = 0.01562
Iteration: 14 - x_14 = [0.17117 7.64542], p_k = [-34.23376 -15.29084], α_k = 0.00781
Iteration: 15 - x_15 = [-0.09628  7.52596], p_k = [ 19.25649 -15.05193], α_k = 0.01562
Iteration: 16 - x_16 = [0.2046  7.29078], p_k = [-40.92004 -14.58155], α_k = 0.00781
Iteration: 17 - x_17 = [-0.11509  7.17686], p_k = [ 23.01752 -14.35372], α_k = 0.00781
Iteration: 18 - x_18 = [0.06474 7.06472], p_k = [-12.94736 -14.12944], α_k = 0.01562
Iteration: 19 - x_19 = [-0.13757  6.84395], p_k = [ 27.51313 -13.68789], α_k = 0.00781
Iteration: 20 - x_20 = [0.07738 6.73701], p_k = [-15.47614 -13.47402], α_k = 0.01562
Iteration: 21 - x_21 = [-0.16443  6.52648], p_k = [ 32.88679 -13.05296], α_k = 0.00781
Iteration: 22 - x_22 = [0.09249 6.4245 ], p_k = [-18.49882 -12.849  ], α_k = 0.00781
Iteration: 23 - x_23 = [-0.05203  6.32412], p_k = [ 10.40559 -12.64824], α_k = 0.01562
Iteration: 24 - x_24 = [0.11056 6.12649], p_k = [-22.11187 -12.25298], α_k = 0.00781
Iteration: 25 - x_25 = [-0.06219  6.03076], p_k = [ 12.43793 -12.06153], α_k = 0.01562
Iteration: 26 - x_26 = [0.13215 5.8423 ], p_k = [-26.4306  -11.68461], α_k = 0.00781
Iteration: 27 - x_27 = [-0.07434  5.75102], p_k = [ 14.86721 -11.50203], α_k = 0.01562
Iteration: 28 - x_28 = [0.15796 5.5713 ], p_k = [-31.59282 -11.1426 ], α_k = 0.00781
Iteration: 29 - x_29 = [-0.08885  5.48425], p_k = [ 17.77096 -10.96849], α_k = 0.00781
Iteration: 30 - x_30 = [0.04998 5.39855], p_k = [ -9.99617 -10.79711], α_k = 0.01562
Iteration: 31 - x_31 = [-0.10621  5.22985], p_k = [ 21.24185 -10.4597 ], α_k = 0.00781
Iteration: 32 - x_32 = [0.05974 5.14813], p_k = [-11.94854 -10.29627], α_k = 0.01562
Iteration: 33 - x_33 = [-0.12695  4.98725], p_k = [25.39065 -9.97451], α_k = 0.00781
Iteration: 34 - x_34 = [0.07141 4.90933], p_k = [-14.28224  -9.81866], α_k = 0.00781
Iteration: 35 - x_35 = [-0.04017  4.83262], p_k = [ 8.03376 -9.66524], α_k = 0.01562
Iteration: 36 - x_36 = [0.08536 4.6816 ], p_k = [-17.07174  -9.3632 ], α_k = 0.00781
Iteration: 37 - x_37 = [-0.04801  4.60845], p_k = [ 9.60286 -9.2169 ], α_k = 0.01562
Iteration: 38 - x_38 = [0.10203 4.46444], p_k = [-20.40607  -8.92887], α_k = 0.00781
Iteration: 39 - x_39 = [-0.05739  4.39468], p_k = [11.47841 -8.78936], α_k = 0.01562
Iteration: 40 - x_40 = [0.12196 4.25735], p_k = [-24.39163  -8.51469], α_k = 0.00781
Iteration: 41 - x_41 = [-0.0686   4.19083], p_k = [13.72029 -8.38165], α_k = 0.00781
Iteration: 42 - x_42 = [0.03859 4.12534], p_k = [-7.71766 -8.25069], α_k = 0.01562
Iteration: 43 - x_43 = [-0.082    3.99643], p_k = [16.40003 -7.99285], α_k = 0.00781
Iteration: 44 - x_44 = [0.04613 3.93398], p_k = [-9.22502 -7.86796], α_k = 0.01562
Iteration: 45 - x_45 = [-0.09802  3.81105], p_k = [19.60317 -7.62209], α_k = 0.00781
Iteration: 46 - x_46 = [0.05513 3.7515 ], p_k = [-11.02678  -7.503  ], α_k = 0.00781
Iteration: 47 - x_47 = [-0.03101  3.69288], p_k = [ 6.20256 -7.38576], α_k = 0.01562
Iteration: 48 - x_48 = [0.0659  3.57748], p_k = [-13.18045  -7.15496], α_k = 0.00781
Iteration: 49 - x_49 = [-0.03707  3.52158], p_k = [ 7.414   -7.04316], α_k = 0.01562
Iteration: 50 - x_50 = [0.07877 3.41153], p_k = [-15.75476  -6.82306], α_k = 0.00781
Iteration: 51 - x_51 = [-0.04431  3.35823], p_k = [ 8.86205 -6.71645], α_k = 0.01562
Iteration: 52 - x_52 = [0.09416 3.25328], p_k = [-18.83186  -6.50656], α_k = 0.00781
Iteration: 53 - x_53 = [-0.05296  3.20245], p_k = [10.59292 -6.4049 ], α_k = 0.00781
Iteration: 54 - x_54 = [0.02979 3.15241], p_k = [-5.95852 -6.30482], α_k = 0.01562
Iteration: 55 - x_55 = [-0.06331  3.0539 ], p_k = [12.66185 -6.10779], α_k = 0.00781
Iteration: 56 - x_56 = [0.03561 3.00618], p_k = [-7.12229 -6.01236], α_k = 0.01562
Iteration: 57 - x_57 = [-0.07567  2.91224], p_k = [15.13487 -5.82447], α_k = 0.00781
Iteration: 58 - x_58 = [0.04257 2.86673], p_k = [-8.51336 -5.73347], α_k = 0.00781
Iteration: 59 - x_59 = [-0.02394  2.82194], p_k = [ 4.78877 -5.64388], α_k = 0.01562
Iteration: 60 - x_60 = [0.05088 2.73376], p_k = [-10.17613  -5.46751], α_k = 0.00781
Iteration: 61 - x_61 = [-0.02862  2.69104], p_k = [ 5.72407 -5.38208], α_k = 0.01562
Iteration: 62 - x_62 = [0.06082 2.60695], p_k = [-12.16365  -5.21389], α_k = 0.00781
Iteration: 63 - x_63 = [-0.03421  2.56621], p_k = [ 6.84205 -5.13242], α_k = 0.00781
Iteration: 64 - x_64 = [0.01924 2.52611], p_k = [-3.84866 -5.05223], α_k = 0.01562
Iteration: 65 - x_65 = [-0.04089  2.44717], p_k = [ 8.17839 -4.89435], α_k = 0.00781
Iteration: 66 - x_66 = [0.023   2.40894], p_k = [-4.60035 -4.81787], α_k = 0.01562
Iteration: 67 - x_67 = [-0.04888  2.33366], p_k = [ 9.77574 -4.66731], α_k = 0.00781
Iteration: 68 - x_68 = [0.02749 2.29719], p_k = [-5.49885 -4.59439], α_k = 0.01562
Iteration: 69 - x_69 = [-0.05843  2.22541], p_k = [11.68506 -4.45081], α_k = 0.00781
Iteration: 70 - x_70 = [0.03286 2.19063], p_k = [-6.57285 -4.38127], α_k = 0.00781
Iteration: 71 - x_71 = [-0.01849  2.15641], p_k = [ 3.69723 -4.31281], α_k = 0.01562
Iteration: 72 - x_72 = [0.03928 2.08902], p_k = [-7.85661 -4.17804], α_k = 0.00781
Iteration: 73 - x_73 = [-0.0221   2.05638], p_k = [ 4.41934 -4.11275], α_k = 0.01562
Iteration: 74 - x_74 = [0.04696 1.99212], p_k = [-9.3911  -3.98423], α_k = 0.00781
Iteration: 75 - x_75 = [-0.02641  1.96099], p_k = [ 5.28249 -3.92198], α_k = 0.00781
Iteration: 76 - x_76 = [0.01486 1.93035], p_k = [-2.9714 -3.8607], α_k = 0.01562
Iteration: 77 - x_77 = [-0.03157  1.87002], p_k = [ 6.31423 -3.74005], α_k = 0.00781
Iteration: 78 - x_78 = [0.01776 1.84081], p_k = [-3.55175 -3.68161], α_k = 0.01562
Iteration: 79 - x_79 = [-0.03774  1.78328], p_k = [ 7.54748 -3.56656], α_k = 0.00781
Iteration: 80 - x_80 = [0.02123 1.75542], p_k = [-4.24546 -3.51083], α_k = 0.01562
Iteration: 81 - x_81 = [-0.04511  1.70056], p_k = [ 9.02159 -3.40112], α_k = 0.00781
Iteration: 82 - x_82 = [0.02537 1.67399], p_k = [-5.07465 -3.34798], α_k = 0.00781
Iteration: 83 - x_83 = [-0.01427  1.64783], p_k = [ 2.85449 -3.29567], α_k = 0.01562
Iteration: 84 - x_84 = [0.03033 1.59634], p_k = [-6.06579 -3.19268], α_k = 0.00781
Iteration: 85 - x_85 = [-0.01706  1.5714 ], p_k = [ 3.41201 -3.14279], α_k = 0.01562
Iteration: 86 - x_86 = [0.03625 1.52229], p_k = [-7.25051 -3.04458], α_k = 0.00781
Iteration: 87 - x_87 = [-0.02039  1.4985 ], p_k = [ 4.07841 -2.99701], α_k = 0.00781
Iteration: 88 - x_88 = [0.01147 1.47509], p_k = [-2.29411 -2.95018], α_k = 0.01562
Iteration: 89 - x_89 = [-0.02437  1.42899], p_k = [ 4.87498 -2.85799], α_k = 0.00781
Iteration: 90 - x_90 = [0.01371 1.40666], p_k = [-2.74218 -2.81333], α_k = 0.01562
Iteration: 91 - x_91 = [-0.02914  1.36271], p_k = [ 5.82712 -2.72541], α_k = 0.00781
Iteration: 92 - x_92 = [0.01639 1.34141], p_k = [-3.27776 -2.68283], α_k = 0.01562
Iteration: 93 - x_93 = [-0.03483  1.29949], p_k = [ 6.96523 -2.59899], α_k = 0.00781
Iteration: 94 - x_94 = [0.01959 1.27919], p_k = [-3.91794 -2.55838], α_k = 0.00781
Iteration: 95 - x_95 = [-0.01102  1.2592 ], p_k = [ 2.20384 -2.51841], α_k = 0.01562
Iteration: 96 - x_96 = [0.02342 1.21985], p_k = [-4.68317 -2.43971], α_k = 0.00781
Iteration: 97 - x_97 = [-0.01317  1.20079], p_k = [ 2.63428 -2.40159], α_k = 0.01562
Iteration: 98 - x_98 = [0.02799 1.16327], p_k = [-5.59785 -2.32654], α_k = 0.00781
Iteration: 99 - x_99 = [-0.01574  1.14509], p_k = [ 3.14879 -2.29018], α_k = 0.00781
Iteration: 100 - x_100 = [0.00886 1.1272 ], p_k = [-1.77119 -2.2544 ], α_k = 0.01562
Iteration: 101 - x_101 = [-0.01882  1.09197], p_k = [ 3.76379 -2.18395], α_k = 0.00781
Iteration: 102 - x_102 = [0.01059 1.07491], p_k = [-2.11713 -2.14983], α_k = 0.01562
Iteration: 103 - x_103 = [-0.02249  1.04132], p_k = [ 4.4989  -2.08264], α_k = 0.00781
Iteration: 104 - x_104 = [0.01265 1.02505], p_k = [-2.53063 -2.0501 ], α_k = 0.01562
Iteration: 105 - x_105 = [-0.02689  0.99302], p_k = [ 5.37759 -1.98604], α_k = 0.00781
Iteration: 106 - x_106 = [0.01512 0.9775 ], p_k = [-3.0249 -1.955 ], α_k = 0.00781
Iteration: 107 - x_107 = [-0.00851  0.96223], p_k = [ 1.7015  -1.92446], α_k = 0.01562
Iteration: 108 - x_108 = [0.01808 0.93216], p_k = [-3.6157  -1.86432], α_k = 0.00781

Iteration: 109 - x_109 = [-0.01017  0.91759], p_k = [ 2.03383 -1.83519], α_k = 0.01562
Iteration: 110 - x_110 = [0.02161 0.88892], p_k = [-4.32189 -1.77784], α_k = 0.00781
Iteration: 111 - x_111 = [-0.01216  0.87503], p_k = [ 2.43106 -1.75006], α_k = 0.00781
Iteration: 112 - x_112 = [0.00684 0.86136], p_k = [-1.36747 -1.72272], α_k = 0.01562
Iteration: 113 - x_113 = [-0.01453  0.83444], p_k = [ 2.90588 -1.66888], α_k = 0.00781
Iteration: 114 - x_114 = [0.00817 0.8214 ], p_k = [-1.63456 -1.6428 ], α_k = 0.01562
Iteration: 115 - x_115 = [-0.01737  0.79573], p_k = [ 3.47343 -1.59147], α_k = 0.00781
Iteration: 116 - x_116 = [0.00977 0.7833 ], p_k = [-1.95381 -1.5666 ], α_k = 0.01562
Iteration: 117 - x_117 = [-0.02076  0.75882], p_k = [ 4.15184 -1.51764], α_k = 0.00781
Iteration: 118 - x_118 = [0.01168 0.74697], p_k = [-2.33541 -1.49393], α_k = 0.00781
Iteration: 119 - x_119 = [-0.00657  0.73529], p_k = [ 1.31367 -1.47059], α_k = 0.01562
Iteration: 120 - x_120 = [0.01396 0.71232], p_k = [-2.79154 -1.42463], α_k = 0.00781
Iteration: 121 - x_121 = [-0.00785  0.70119], p_k = [ 1.57024 -1.40237], α_k = 0.01562
Iteration: 122 - x_122 = [0.01668 0.67927], p_k = [-3.33677 -1.35855], α_k = 0.00781
Iteration: 123 - x_123 = [-0.00938  0.66866], p_k = [ 1.87693 -1.33732], α_k = 0.00781
Iteration: 124 - x_124 = [0.00528 0.65821], p_k = [-1.05577 -1.31642], α_k = 0.01562
Iteration: 125 - x_125 = [-0.01122  0.63764], p_k = [ 2.24352 -1.27529], α_k = 0.00781
Iteration: 126 - x_126 = [0.00631 0.62768], p_k = [-1.26198 -1.25536], α_k = 0.01562
Iteration: 127 - x_127 = [-0.01341  0.60807], p_k = [ 2.68171 -1.21613], α_k = 0.00781
Iteration: 128 - x_128 = [0.00754 0.59856], p_k = [-1.50846 -1.19713], α_k = 0.01562
Iteration: 129 - x_129 = [-0.01603  0.57986], p_k = [ 3.20548 -1.15972], α_k = 0.00781
Iteration: 130 - x_130 = [0.00902 0.5708 ], p_k = [-1.80308 -1.1416 ], α_k = 0.00781
Iteration: 131 - x_131 = [-0.00507  0.56188], p_k = [ 1.01423 -1.12376], α_k = 0.01562
Iteration: 132 - x_132 = [0.01078 0.54432], p_k = [-2.15525 -1.08864], α_k = 0.00781
Iteration: 133 - x_133 = [-0.00606  0.53582], p_k = [ 1.21233 -1.07163], α_k = 0.01562
Iteration: 134 - x_134 = [0.01288 0.51907], p_k = [-2.57619 -1.03814], α_k = 0.00781
Iteration: 135 - x_135 = [-0.00725  0.51096], p_k = [ 1.44911 -1.02192], α_k = 0.00781
Iteration: 136 - x_136 = [0.00408 0.50298], p_k = [-0.81512 -1.00596], α_k = 0.01562
Iteration: 137 - x_137 = [-0.00866  0.48726], p_k = [ 1.73214 -0.97452], α_k = 0.00781
Iteration: 138 - x_138 = [0.00487 0.47965], p_k = [-0.97433 -0.95929], α_k = 0.01562
Iteration: 139 - x_139 = [-0.01035  0.46466], p_k = [ 2.07044 -0.92931], α_k = 0.00781
Iteration: 140 - x_140 = [0.00582 0.4574 ], p_k = [-1.16463 -0.91479], α_k = 0.01562
Iteration: 141 - x_141 = [-0.01237  0.4431 ], p_k = [ 2.47483 -0.88621], α_k = 0.00781
Iteration: 142 - x_142 = [0.00696 0.43618], p_k = [-1.39209 -0.87236], α_k = 0.00781
Iteration: 143 - x_143 = [-0.00392  0.42936], p_k = [ 0.78305 -0.85873], α_k = 0.01562
Iteration: 144 - x_144 = [0.00832 0.41595], p_k = [-1.66398 -0.83189], α_k = 0.00781
Iteration: 145 - x_145 = [-0.00468  0.40945], p_k = [ 0.93599 -0.8189 ], α_k = 0.01562
Iteration: 146 - x_146 = [0.00994 0.39665], p_k = [-1.98898 -0.7933 ], α_k = 0.00781
Iteration: 147 - x_147 = [-0.00559  0.39045], p_k = [ 1.1188  -0.78091], α_k = 0.00781
Iteration: 148 - x_148 = [0.00315 0.38435], p_k = [-0.62933 -0.76871], α_k = 0.01562
Iteration: 149 - x_149 = [-0.00669  0.37234], p_k = [ 1.33732 -0.74469], α_k = 0.00781
Iteration: 150 - x_150 = [0.00376 0.36652], p_k = [-0.75224 -0.73305], α_k = 0.01562
Iteration: 151 - x_151 = [-0.00799  0.35507], p_k = [ 1.59851 -0.71014], α_k = 0.00781
Iteration: 152 - x_152 = [0.0045  0.34952], p_k = [-0.89916 -0.69905], α_k = 0.01562
Iteration: 153 - x_153 = [-0.00955  0.3386 ], p_k = [ 1.91072 -0.6772 ], α_k = 0.00781
Iteration: 154 - x_154 = [0.00537 0.33331], p_k = [-1.07478 -0.66662], α_k = 0.00781
Iteration: 155 - x_155 = [-0.00302  0.3281 ], p_k = [ 0.60456 -0.6562 ], α_k = 0.01562
Iteration: 156 - x_156 = [0.00642 0.31785], p_k = [-1.2847 -0.6357], α_k = 0.00781
Iteration: 157 - x_157 = [-0.00361  0.31288], p_k = [ 0.72264 -0.62576], α_k = 0.01562
Iteration: 158 - x_158 = [0.00768 0.3031 ], p_k = [-1.53562 -0.60621], α_k = 0.00781
Iteration: 159 - x_159 = [-0.00432  0.29837], p_k = [ 0.86378 -0.59674], α_k = 0.00781
Iteration: 160 - x_160 = [0.00243 0.29371], p_k = [-0.48588 -0.58741], α_k = 0.01562
Iteration: 161 - x_161 = [-0.00516  0.28453], p_k = [ 1.03249 -0.56906], α_k = 0.00781
Iteration: 162 - x_162 = [0.0029  0.28008], p_k = [-0.58078 -0.56017], α_k = 0.01562
Iteration: 163 - x_163 = [-0.00617  0.27133], p_k = [ 1.23415 -0.54266], α_k = 0.00781
Iteration: 164 - x_164 = [0.00347 0.26709], p_k = [-0.69421 -0.53418], α_k = 0.01562
Iteration: 165 - x_165 = [-0.00738  0.25874], p_k = [ 1.4752  -0.51749], α_k = 0.00781
Iteration: 166 - x_166 = [0.00415 0.2547 ], p_k = [-0.8298 -0.5094], α_k = 0.00781
Iteration: 167 - x_167 = [-0.00233  0.25072], p_k = [ 0.46676 -0.50144], α_k = 0.01562
Iteration: 168 - x_168 = [0.00496 0.24289], p_k = [-0.99187 -0.48577], α_k = 0.00781
Iteration: 169 - x_169 = [-0.00279  0.23909], p_k = [ 0.55793 -0.47818], α_k = 0.01562
Iteration: 170 - x_170 = [0.00593 0.23162], p_k = [-1.18559 -0.46324], α_k = 0.00781
Iteration: 171 - x_171 = [-0.00333  0.228  ], p_k = [ 0.6669 -0.456 ], α_k = 0.00781
Iteration: 172 - x_172 = [0.00188 0.22444], p_k = [-0.37513 -0.44888], α_k = 0.01562
Iteration: 173 - x_173 = [-0.00399  0.21742], p_k = [ 0.79715 -0.43485], α_k = 0.00781
Iteration: 174 - x_174 = [0.00224 0.21403], p_k = [-0.4484  -0.42805], α_k = 0.01562
Iteration: 175 - x_175 = [-0.00476  0.20734], p_k = [ 0.95284 -0.41468], α_k = 0.00781
Iteration: 176 - x_176 = [0.00268 0.2041 ], p_k = [-0.53597 -0.4082 ], α_k = 0.01562
Iteration: 177 - x_177 = [-0.00569  0.19772], p_k = [ 1.13894 -0.39544], α_k = 0.00781
Iteration: 178 - x_178 = [0.0032  0.19463], p_k = [-0.64066 -0.38926], α_k = 0.00781
Iteration: 179 - x_179 = [-0.0018   0.19159], p_k = [ 0.36037 -0.38318], α_k = 0.01562
Iteration: 180 - x_180 = [0.00383 0.1856 ], p_k = [-0.76578 -0.37121], α_k = 0.00781
Iteration: 181 - x_181 = [-0.00215  0.1827 ], p_k = [ 0.43075 -0.36541], α_k = 0.01562
Iteration: 182 - x_182 = [0.00458 0.17699], p_k = [-0.91535 -0.35399], α_k = 0.00781
Iteration: 183 - x_183 = [-0.00257  0.17423], p_k = [ 0.51488 -0.34846], α_k = 0.00781
Iteration: 184 - x_184 = [0.00145 0.17151], p_k = [-0.28962 -0.34301], α_k = 0.01562
Iteration: 185 - x_185 = [-0.00308  0.16615], p_k = [ 0.61545 -0.33229], α_k = 0.00781
Iteration: 186 - x_186 = [0.00173 0.16355], p_k = [-0.34619 -0.3271 ], α_k = 0.01562
Iteration: 187 - x_187 = [-0.00368  0.15844], p_k = [ 0.73565 -0.31688], α_k = 0.00781
Iteration: 188 - x_188 = [0.00207 0.15596], p_k = [-0.4138  -0.31193], α_k = 0.00781
Iteration: 189 - x_189 = [-0.00116  0.15353], p_k = [ 0.23277 -0.30705], α_k = 0.01562
Iteration: 190 - x_190 = [0.00247 0.14873], p_k = [-0.49463 -0.29746], α_k = 0.00781
Iteration: 191 - x_191 = [-0.00139  0.14641], p_k = [ 0.27823 -0.29281], α_k = 0.01562
Iteration: 192 - x_192 = [0.00296 0.14183], p_k = [-0.59123 -0.28366], α_k = 0.00781
Iteration: 193 - x_193 = [-0.00166  0.13961], p_k = [ 0.33257 -0.27923], α_k = 0.01562
Iteration: 194 - x_194 = [0.00353 0.13525], p_k = [-0.70671 -0.2705 ], α_k = 0.00781
Iteration: 195 - x_195 = [-0.00199  0.13314], p_k = [ 0.39752 -0.26628], α_k = 0.00781
Iteration: 196 - x_196 = [0.00112 0.13106], p_k = [-0.22361 -0.26211], α_k = 0.01562
Iteration: 197 - x_197 = [-0.00238  0.12696], p_k = [ 0.47516 -0.25392], α_k = 0.00781
Iteration: 198 - x_198 = [0.00134 0.12498], p_k = [-0.26728 -0.24996], α_k = 0.01562
Iteration: 199 - x_199 = [-0.00284  0.12107], p_k = [ 0.56797 -0.24215], α_k = 0.00781
Iteration: 200 - x_200 = [0.0016  0.11918], p_k = [-0.31948 -0.23836], α_k = 0.00781
Iteration: 201 - x_201 = [-0.0009   0.11732], p_k = [ 0.17971 -0.23464], α_k = 0.01562
Iteration: 202 - x_202 = [0.00191 0.11365], p_k = [-0.38188 -0.2273 ], α_k = 0.00781
Iteration: 203 - x_203 = [-0.00107  0.11188], p_k = [ 0.21481 -0.22375], α_k = 0.01562
Iteration: 204 - x_204 = [0.00228 0.10838], p_k = [-0.45647 -0.21676], α_k = 0.00781
Iteration: 205 - x_205 = [-0.00128  0.10669], p_k = [ 0.25676 -0.21337], α_k = 0.01562
Iteration: 206 - x_206 = [0.00273 0.10335], p_k = [-0.54562 -0.20671], α_k = 0.00781
Iteration: 207 - x_207 = [-0.00153  0.10174], p_k = [ 0.30691 -0.20348], α_k = 0.00781

Iteration: 208 - x_208 = [0.00086 0.10015], p_k = [-0.17264 -0.2003 ], α_k = 0.01562
Iteration: 209 - x_209 = [-0.00183  0.09702], p_k = [ 0.36686 -0.19404], α_k = 0.00781
Iteration: 210 - x_210 = [0.00103 0.0955 ], p_k = [-0.20636 -0.19101], α_k = 0.01562
Iteration: 211 - x_211 = [-0.00219  0.09252], p_k = [ 0.43851 -0.18504], α_k = 0.00781
Iteration: 212 - x_212 = [0.00123 0.09107], p_k = [-0.24666 -0.18215], α_k = 0.00781
Iteration: 213 - x_213 = [-0.00069  0.08965], p_k = [ 0.13875 -0.1793 ], α_k = 0.01562
Iteration: 214 - x_214 = [0.00147 0.08685], p_k = [-0.29484 -0.1737 ], α_k = 0.00781
Iteration: 215 - x_215 = [-0.00083  0.08549], p_k = [ 0.16585 -0.17098], α_k = 0.01562
Iteration: 216 - x_216 = [0.00176 0.08282], p_k = [-0.35242 -0.16564], α_k = 0.00781
Iteration: 217 - x_217 = [-0.00099  0.08153], p_k = [ 0.19824 -0.16305], α_k = 0.01562
Iteration: 218 - x_218 = [0.00211 0.07898], p_k = [-0.42125 -0.15796], α_k = 0.00781
Iteration: 219 - x_219 = [-0.00118  0.07774], p_k = [ 0.23696 -0.15549], α_k = 0.00781
Iteration: 220 - x_220 = [0.00067 0.07653], p_k = [-0.13329 -0.15306], α_k = 0.01562
Iteration: 221 - x_221 = [-0.00142  0.07414], p_k = [ 0.28324 -0.14828], α_k = 0.00781
Iteration: 222 - x_222 = [0.0008  0.07298], p_k = [-0.15932 -0.14596], α_k = 0.01562
Iteration: 223 - x_223 = [-0.00169  0.0707 ], p_k = [ 0.33856 -0.1414 ], α_k = 0.00781
Iteration: 224 - x_224 = [0.00095 0.06959], p_k = [-0.19044 -0.13919], α_k = 0.00781
Iteration: 225 - x_225 = [-0.00054  0.06851], p_k = [ 0.10712 -0.13701], α_k = 0.01562
Iteration: 226 - x_226 = [0.00114 0.06637], p_k = [-0.22763 -0.13273], α_k = 0.00781
Iteration: 227 - x_227 = [-0.00064  0.06533], p_k = [ 0.12804 -0.13066], α_k = 0.01562
Iteration: 228 - x_228 = [0.00136 0.06329], p_k = [-0.27209 -0.12657], α_k = 0.00781
Iteration: 229 - x_229 = [-0.00077  0.0623 ], p_k = [ 0.15305 -0.1246 ], α_k = 0.01562
Iteration: 230 - x_230 = [0.00163 0.06035], p_k = [-0.32523 -0.1207 ], α_k = 0.00781
Iteration: 231 - x_231 = [-0.00091  0.05941], p_k = [ 0.18294 -0.11882], α_k = 0.00781
Iteration: 232 - x_232 = [0.00051 0.05848], p_k = [-0.10291 -0.11696], α_k = 0.01562
Iteration: 233 - x_233 = [-0.00109  0.05665], p_k = [ 0.21868 -0.11331], α_k = 0.00781
Iteration: 234 - x_234 = [0.00062 0.05577], p_k = [-0.12301 -0.11154], α_k = 0.01562
Iteration: 235 - x_235 = [-0.00131  0.05402], p_k = [ 0.26139 -0.10805], α_k = 0.00781
Iteration: 236 - x_236 = [0.00074 0.05318], p_k = [-0.14703 -0.10636], α_k = 0.00781
Iteration: 237 - x_237 = [-0.00041  0.05235], p_k = [ 0.0827 -0.1047], α_k = 0.01562
Iteration: 238 - x_238 = [0.00088 0.05071], p_k = [-0.17575 -0.10143], α_k = 0.00781
Iteration: 239 - x_239 = [-0.00049  0.04992], p_k = [ 0.09886 -0.09984], α_k = 0.01562
Iteration: 240 - x_240 = [0.00105 0.04836], p_k = [-0.21007 -0.09672], α_k = 0.00781
Iteration: 241 - x_241 = [-0.00059  0.04761], p_k = [ 0.11817 -0.09521], α_k = 0.01562
Iteration: 242 - x_242 = [0.00126 0.04612], p_k = [-0.2511  -0.09224], α_k = 0.00781
Iteration: 243 - x_243 = [-0.00071  0.0454 ], p_k = [ 0.14124 -0.09079], α_k = 0.00781
Iteration: 244 - x_244 = [0.0004  0.04469], p_k = [-0.07945 -0.08938], α_k = 0.01562
Iteration: 245 - x_245 = [-0.00084  0.04329], p_k = [ 0.16883 -0.08658], α_k = 0.00781
Iteration: 246 - x_246 = [0.00047 0.04262], p_k = [-0.09497 -0.08523], α_k = 0.01562
Iteration: 247 - x_247 = [-0.00101  0.04128], p_k = [ 0.20181 -0.08257], α_k = 0.00781
Iteration: 248 - x_248 = [0.00057 0.04064], p_k = [-0.11352 -0.08128], α_k = 0.00781
Iteration: 249 - x_249 = [-0.00032  0.04   ], p_k = [ 0.06385 -0.08001], α_k = 0.01562
Iteration: 250 - x_250 = [0.00068 0.03875], p_k = [-0.13569 -0.07751], α_k = 0.00781
Iteration: 251 - x_251 = [-0.00038  0.03815], p_k = [ 0.07632 -0.0763 ], α_k = 0.01562
Iteration: 252 - x_252 = [0.00081 0.03696], p_k = [-0.16219 -0.07391], α_k = 0.00781
Iteration: 253 - x_253 = [-0.00046  0.03638], p_k = [ 0.09123 -0.07276], α_k = 0.01562
Iteration: 254 - x_254 = [0.00097 0.03524], p_k = [-0.19387 -0.07048], α_k = 0.00781
Iteration: 255 - x_255 = [-0.00055  0.03469], p_k = [ 0.10905 -0.06938], α_k = 0.00781
Iteration: 256 - x_256 = [0.00031 0.03415], p_k = [-0.06134 -0.0683 ], α_k = 0.01562
Iteration: 257 - x_257 = [-0.00065  0.03308], p_k = [ 0.13035 -0.06616], α_k = 0.00781
Iteration: 258 - x_258 = [0.00037 0.03256], p_k = [-0.07332 -0.06513], α_k = 0.01562
Iteration: 259 - x_259 = [-0.00078  0.03155], p_k = [ 0.15581 -0.06309], α_k = 0.00781
Iteration: 260 - x_260 = [0.00044 0.03105], p_k = [-0.08764 -0.06211], α_k = 0.00781
Iteration: 261 - x_261 = [-0.00025  0.03057], p_k = [ 0.0493  -0.06114], α_k = 0.01562
Iteration: 262 - x_262 = [0.00052 0.02961], p_k = [-0.10476 -0.05923], α_k = 0.00781
Iteration: 263 - x_263 = [-0.00029  0.02915], p_k = [ 0.05893 -0.0583 ], α_k = 0.01562
Iteration: 264 - x_264 = [0.00063 0.02824], p_k = [-0.12522 -0.05648], α_k = 0.00781
Iteration: 265 - x_265 = [-0.00035  0.0278 ], p_k = [ 0.07044 -0.0556 ], α_k = 0.01562
Iteration: 266 - x_266 = [0.00075 0.02693], p_k = [-0.14968 -0.05386], α_k = 0.00781
Iteration: 267 - x_267 = [-0.00042  0.02651], p_k = [ 0.08419 -0.05302], α_k = 0.00781
Iteration: 268 - x_268 = [0.00024 0.0261 ], p_k = [-0.04736 -0.05219], α_k = 0.01562
Iteration: 269 - x_269 = [-0.0005   0.02528], p_k = [ 0.10064 -0.05056], α_k = 0.00781
Iteration: 270 - x_270 = [0.00028 0.02488], p_k = [-0.05661 -0.04977], α_k = 0.01562
Iteration: 271 - x_271 = [-0.0006   0.02411], p_k = [ 0.12029 -0.04821], α_k = 0.00781
Iteration: 272 - x_272 = [0.00034 0.02373], p_k = [-0.06766 -0.04746], α_k = 0.00781
Iteration: 273 - x_273 = [-0.00019  0.02336], p_k = [ 0.03806 -0.04672], α_k = 0.01562
Iteration: 274 - x_274 = [0.0004  0.02263], p_k = [-0.08088 -0.04526], α_k = 0.00781
Iteration: 275 - x_275 = [-0.00023  0.02228], p_k = [ 0.0455  -0.04455], α_k = 0.01562
Iteration: 276 - x_276 = [0.00048 0.02158], p_k = [-0.09668 -0.04316], α_k = 0.00781
Iteration: 277 - x_277 = [-0.00027  0.02124], p_k = [ 0.05438 -0.04249], α_k = 0.01562
Iteration: 278 - x_278 = [0.00058 0.02058], p_k = [-0.11556 -0.04116], α_k = 0.00781
Iteration: 279 - x_279 = [-0.00033  0.02026], p_k = [ 0.065   -0.04051], α_k = 0.00781
Iteration: 280 - x_280 = [0.00018 0.01994], p_k = [-0.03656 -0.03988], α_k = 0.01562
Iteration: 281 - x_281 = [-0.00039  0.01932], p_k = [ 0.0777  -0.03864], α_k = 0.00781
Iteration: 282 - x_282 = [0.00022 0.01902], p_k = [-0.04371 -0.03803], α_k = 0.01562
Iteration: 283 - x_283 = [-0.00046  0.01842], p_k = [ 0.09287 -0.03684], α_k = 0.00781
Iteration: 284 - x_284 = [0.00026 0.01813], p_k = [-0.05224 -0.03627], α_k = 0.00781
Iteration: 285 - x_285 = [-0.00015  0.01785], p_k = [ 0.02939 -0.0357 ], α_k = 0.01562
Iteration: 286 - x_286 = [0.00031 0.01729], p_k = [-0.06244 -0.03458], α_k = 0.00781
Iteration: 287 - x_287 = [-0.00018  0.01702], p_k = [ 0.03513 -0.03404], α_k = 0.01562
Iteration: 288 - x_288 = [0.00037 0.01649], p_k = [-0.07464 -0.03298], α_k = 0.00781
Iteration: 289 - x_289 = [-0.00021  0.01623], p_k = [ 0.04199 -0.03247], α_k = 0.01562
Iteration: 290 - x_290 = [0.00045 0.01573], p_k = [-0.08922 -0.03145], α_k = 0.00781
Iteration: 291 - x_291 = [-0.00025  0.01548], p_k = [ 0.05019 -0.03096], α_k = 0.00781
Iteration: 292 - x_292 = [0.00014 0.01524], p_k = [-0.02823 -0.03048], α_k = 0.01562
Iteration: 293 - x_293 = [-0.0003   0.01476], p_k = [ 0.05999 -0.02952], α_k = 0.00781
Iteration: 294 - x_294 = [0.00017 0.01453], p_k = [-0.03374 -0.02906], α_k = 0.01562
Iteration: 295 - x_295 = [-0.00036  0.01408], p_k = [ 0.0717  -0.02815], α_k = 0.00781
Iteration: 296 - x_296 = [0.0002  0.01386], p_k = [-0.04033 -0.02771], α_k = 0.00781
Iteration: 297 - x_297 = [-0.00011  0.01364], p_k = [ 0.02269 -0.02728], α_k = 0.01562
Iteration: 298 - x_298 = [0.00024 0.01321], p_k = [-0.04821 -0.02643], α_k = 0.00781
Iteration: 299 - x_299 = [-0.00014  0.01301], p_k = [ 0.02712 -0.02602], α_k = 0.01562
Iteration: 300 - x_300 = [0.00029 0.0126 ], p_k = [-0.05763 -0.0252 ], α_k = 0.00781
Iteration: 301 - x_301 = [-0.00016  0.0124 ], p_k = [ 0.03242 -0.02481], α_k = 0.01562
Iteration: 302 - x_302 = [0.00034 0.01202], p_k = [-0.06888 -0.02403], α_k = 0.00781
Iteration: 303 - x_303 = [-0.00019  0.01183], p_k = [ 0.03875 -0.02366], α_k = 0.00781
Iteration: 304 - x_304 = [0.00011 0.01164], p_k = [-0.02179 -0.02329], α_k = 0.01562
Iteration: 305 - x_305 = [-0.00023  0.01128], p_k = [ 0.04631 -0.02256], α_k = 0.00781
Iteration: 306 - x_306 = [0.00013 0.0111 ], p_k = [-0.02605 -0.02221], α_k = 0.01562
Iteration: 307 - x_307 = [-0.00028  0.01076], p_k = [ 0.05536 -0.02151], α_k = 0.00781
Iteration: 308 - x_308 = [0.00016 0.01059], p_k = [-0.03114 -0.02118], α_k = 0.00781
Iteration: 309 - x_309 = [-9.000e-05  1.042e-02], p_k = [ 0.01752 -0.02085], α_k = 0.01562
Iteration: 310 - x_310 = [0.00019 0.0101 ], p_k = [-0.03722 -0.0202 ], α_k = 0.00781
Iteration: 311 - x_311 = [-0.0001   0.00994], p_k = [ 0.02094 -0.01988], α_k = 0.01562
Iteration: 312 - x_312 = [0.00022 0.00963], p_k = [-0.04449 -0.01926], α_k = 0.00781
Iteration: 313 - x_313 = [-0.00013  0.00948], p_k = [ 0.02503 -0.01896], α_k = 0.01562
Iteration: 314 - x_314 = [0.00027 0.00918], p_k = [-0.05318 -0.01837], α_k = 0.00781
Iteration: 315 - x_315 = [-0.00015  0.00904], p_k = [ 0.02991 -0.01808], α_k = 0.00781
Iteration: 316 - x_316 = [8.0e-05 8.9e-03], p_k = [-0.01683 -0.0178 ], α_k = 0.01562
Iteration: 317 - x_317 = [-0.00018  0.00862], p_k = [ 0.03576 -0.01724], α_k = 0.00781
Iteration: 318 - x_318 = [0.0001  0.00849], p_k = [-0.02011 -0.01697], α_k = 0.01562
Iteration: 319 - x_319 = [-0.00021  0.00822], p_k = [ 0.04274 -0.01644], α_k = 0.00781
Iteration: 320 - x_320 = [0.00012 0.00809], p_k = [-0.02404 -0.01618], α_k = 0.00781
Iteration: 321 - x_321 = [-7.00e-05  7.97e-03], p_k = [ 0.01352 -0.01593], α_k = 0.01562
Iteration: 322 - x_322 = [0.00014 0.00772], p_k = [-0.02874 -0.01543], α_k = 0.00781
Iteration: 323 - x_323 = [-8.0e-05  7.6e-03], p_k = [ 0.01616 -0.01519], α_k = 0.01562
Iteration: 324 - x_324 = [0.00017 0.00736], p_k = [-0.03435 -0.01472], α_k = 0.00781
Iteration: 325 - x_325 = [-0.0001   0.00724], p_k = [ 0.01932 -0.01449], α_k = 0.00781
Iteration: 326 - x_326 = [5.00e-05 7.13e-03], p_k = [-0.01087 -0.01426], α_k = 0.01562

Iteration: 327 - x_327 = [-0.00012  0.00691], p_k = [ 0.0231  -0.01381], α_k = 0.00781
Iteration: 328 - x_328 = [6.0e-05 6.8e-03], p_k = [-0.01299 -0.0136 ], α_k = 0.01562
Iteration: 329 - x_329 = [-0.00014  0.00659], p_k = [ 0.02761 -0.01317], α_k = 0.00781
Iteration: 330 - x_330 = [8.00e-05 6.48e-03], p_k = [-0.01553 -0.01297], α_k = 0.01562
Iteration: 331 - x_331 = [-0.00016  0.00628], p_k = [ 0.033   -0.01256], α_k = 0.00781
Iteration: 332 - x_332 = [9.00e-05 6.18e-03], p_k = [-0.01856 -0.01237], α_k = 0.00781
Iteration: 333 - x_333 = [-5.00e-05  6.09e-03], p_k = [ 0.01044 -0.01217], α_k = 0.01562
Iteration: 334 - x_334 = [0.00011 0.0059 ], p_k = [-0.02219 -0.01179], α_k = 0.00781
Iteration: 335 - x_335 = [-6.0e-05  5.8e-03], p_k = [ 0.01248 -0.01161], α_k = 0.01562
Iteration: 336 - x_336 = [0.00013 0.00562], p_k = [-0.02652 -0.01125], α_k = 0.00781
Iteration: 337 - x_337 = [-7.00e-05  5.54e-03], p_k = [ 0.01492 -0.01107], α_k = 0.00781
Iteration: 338 - x_338 = [4.00e-05 5.45e-03], p_k = [-0.00839 -0.0109 ], α_k = 0.01562
Iteration: 339 - x_339 = [-9.00e-05  5.28e-03], p_k = [ 0.01783 -0.01056], α_k = 0.00781
Iteration: 340 - x_340 = [5.0e-05 5.2e-03], p_k = [-0.01003 -0.01039], α_k = 0.01562
Iteration: 341 - x_341 = [-0.00011  0.00503], p_k = [ 0.02131 -0.01007], α_k = 0.00781
Iteration: 342 - x_342 = [6.00e-05 4.95e-03], p_k = [-0.01199 -0.00991], α_k = 0.01562
Iteration: 343 - x_343 = [-0.00013  0.0048 ], p_k = [ 0.02548 -0.0096 ], α_k = 0.00781
Iteration: 344 - x_344 = [7.00e-05 4.72e-03], p_k = [-0.01433 -0.00945], α_k = 0.00781
Iteration: 345 - x_345 = [-4.00e-05  4.65e-03], p_k = [ 0.00806 -0.0093 ], α_k = 0.01562
Iteration: 346 - x_346 = [9.00e-05 4.51e-03], p_k = [-0.01713 -0.00901], α_k = 0.00781
Iteration: 347 - x_347 = [-5.00e-05  4.44e-03], p_k = [ 0.00964 -0.00887], α_k = 0.01562
Iteration: 348 - x_348 = [0.0001 0.0043], p_k = [-0.02048 -0.00859], α_k = 0.00781
Iteration: 349 - x_349 = [-6.00e-05  4.23e-03], p_k = [ 0.01152 -0.00846], α_k = 0.00781
Iteration: 350 - x_350 = [3.00e-05 4.16e-03], p_k = [-0.00648 -0.00833], α_k = 0.01562
Iteration: 351 - x_351 = [-7.00e-05  4.03e-03], p_k = [ 0.01377 -0.00807], α_k = 0.00781
Iteration: 352 - x_352 = [4.00e-05 3.97e-03], p_k = [-0.00774 -0.00794], α_k = 0.01562
Iteration: 353 - x_353 = [-8.00e-05  3.85e-03], p_k = [ 0.01646 -0.00769], α_k = 0.00781
Iteration: 354 - x_354 = [5.00e-05 3.79e-03], p_k = [-0.00926 -0.00757], α_k = 0.01562
Iteration: 355 - x_355 = [-0.0001   0.00367], p_k = [ 0.01967 -0.00734], α_k = 0.00781
Iteration: 356 - x_356 = [6.00e-05 3.61e-03], p_k = [-0.01106 -0.00722], α_k = 0.00781
Iteration: 357 - x_357 = [-3.00e-05  3.55e-03], p_k = [ 0.00622 -0.00711], α_k = 0.01562
Iteration: 358 - x_358 = [7.00e-05 3.44e-03], p_k = [-0.01323 -0.00689], α_k = 0.00781
Iteration: 359 - x_359 = [-4.00e-05  3.39e-03], p_k = [ 0.00744 -0.00678], α_k = 0.01562
Iteration: 360 - x_360 = [8.00e-05 3.28e-03], p_k = [-0.01581 -0.00657], α_k = 0.00781
Iteration: 361 - x_361 = [-4.00e-05  3.23e-03], p_k = [ 0.00889 -0.00646], α_k = 0.00781
Iteration: 362 - x_362 = [3.00e-05 3.18e-03], p_k = [-0.005   -0.00636], α_k = 0.01562
Iteration: 363 - x_363 = [-5.00e-05  3.08e-03], p_k = [ 0.01063 -0.00616], α_k = 0.00781
Iteration: 364 - x_364 = [3.00e-05 3.03e-03], p_k = [-0.00598 -0.00607], α_k = 0.01562
Iteration: 365 - x_365 = [-6.00e-05  2.94e-03], p_k = [ 0.01271 -0.00588], α_k = 0.00781
Iteration: 366 - x_366 = [4.00e-05 2.89e-03], p_k = [-0.00715 -0.00579], α_k = 0.01562
Iteration: 367 - x_367 = [-8.0e-05  2.8e-03], p_k = [ 0.01519 -0.00561], α_k = 0.00781
Iteration: 368 - x_368 = [4.00e-05 2.76e-03], p_k = [-0.00854 -0.00552], α_k = 0.00781
Iteration: 369 - x_369 = [-2.00e-05  2.72e-03], p_k = [ 0.00481 -0.00543], α_k = 0.01562
Iteration: 370 - x_370 = [5.00e-05 2.63e-03], p_k = [-0.01021 -0.00526], α_k = 0.00781
Iteration: 371 - x_371 = [-3.00e-05  2.59e-03], p_k = [ 0.00574 -0.00518], α_k = 0.01562
Iteration: 372 - x_372 = [6.00e-05 2.51e-03], p_k = [-0.01221 -0.00502], α_k = 0.00781
Iteration: 373 - x_373 = [-3.00e-05  2.47e-03], p_k = [ 0.00687 -0.00494], α_k = 0.00781
Iteration: 374 - x_374 = [2.00e-05 2.43e-03], p_k = [-0.00386 -0.00486], α_k = 0.01562
Iteration: 375 - x_375 = [-4.00e-05  2.36e-03], p_k = [ 0.00821 -0.00471], α_k = 0.00781
Iteration: 376 - x_376 = [2.00e-05 2.32e-03], p_k = [-0.00462 -0.00464], α_k = 0.01562
Iteration: 377 - x_377 = [-5.00e-05  2.25e-03], p_k = [ 0.00981 -0.00449], α_k = 0.00781
Iteration: 378 - x_378 = [3.00e-05 2.21e-03], p_k = [-0.00552 -0.00442], α_k = 0.01562
Iteration: 379 - x_379 = [-6.00e-05  2.14e-03], p_k = [ 0.01172 -0.00428], α_k = 0.00781
Iteration: 380 - x_380 = [3.00e-05 2.11e-03], p_k = [-0.0066  -0.00422], α_k = 0.00781
Iteration: 381 - x_381 = [-2.00e-05  2.08e-03], p_k = [ 0.00371 -0.00415], α_k = 0.01562
Iteration: 382 - x_382 = [4.00e-05 2.01e-03], p_k = [-0.00788 -0.00402], α_k = 0.00781
Iteration: 383 - x_383 = [-2.00e-05  1.98e-03], p_k = [ 0.00443 -0.00396], α_k = 0.01562
Iteration: 384 - x_384 = [5.00e-05 1.92e-03], p_k = [-0.00942 -0.00383], α_k = 0.00781
Iteration: 385 - x_385 = [-3.00e-05  1.89e-03], p_k = [ 0.0053  -0.00377], α_k = 0.00781
Iteration: 386 - x_386 = [1.00e-05 1.86e-03], p_k = [-0.00298 -0.00372], α_k = 0.01562
Iteration: 387 - x_387 = [-3.0e-05  1.8e-03], p_k = [ 0.00634 -0.0036 ], α_k = 0.00781
Iteration: 388 - x_388 = [2.00e-05 1.77e-03], p_k = [-0.00356 -0.00354], α_k = 0.01562
Iteration: 389 - x_389 = [-4.00e-05  1.72e-03], p_k = [ 0.00757 -0.00343], α_k = 0.00781
Iteration: 390 - x_390 = [2.00e-05 1.69e-03], p_k = [-0.00426 -0.00338], α_k = 0.01562
Iteration: 391 - x_391 = [-5.00e-05  1.64e-03], p_k = [ 0.00905 -0.00327], α_k = 0.00781
Iteration: 392 - x_392 = [3.00e-05 1.61e-03], p_k = [-0.00509 -0.00322], α_k = 0.00781
Iteration: 393 - x_393 = [-1.00e-05  1.59e-03], p_k = [ 0.00286 -0.00317], α_k = 0.01562
Iteration: 394 - x_394 = [3.00e-05 1.54e-03], p_k = [-0.00609 -0.00307], α_k = 0.00781
Iteration: 395 - x_395 = [-2.00e-05  1.51e-03], p_k = [ 0.00342 -0.00302], α_k = 0.01562
Iteration: 396 - x_396 = [4.00e-05 1.47e-03], p_k = [-0.00728 -0.00293], α_k = 0.00781
Iteration: 397 - x_397 = [-2.00e-05  1.44e-03], p_k = [ 0.00409 -0.00288], α_k = 0.00781
Iteration: 398 - x_398 = [1.00e-05 1.42e-03], p_k = [-0.0023  -0.00284], α_k = 0.01562
Iteration: 399 - x_399 = [-2.00e-05  1.38e-03], p_k = [ 0.00489 -0.00275], α_k = 0.00781
Iteration: 400 - x_400 = [1.00e-05 1.35e-03], p_k = [-0.00275 -0.00271], α_k = 0.01562
Iteration: 401 - x_401 = [-3.00e-05  1.31e-03], p_k = [ 0.00585 -0.00262], α_k = 0.00781
Iteration: 402 - x_402 = [2.00e-05 1.29e-03], p_k = [-0.00329 -0.00258], α_k = 0.01562
Iteration: 403 - x_403 = [-3.00e-05  1.25e-03], p_k = [ 0.00699 -0.0025 ], α_k = 0.00781
Iteration: 404 - x_404 = [2.00e-05 1.23e-03], p_k = [-0.00393 -0.00246], α_k = 0.00781
Iteration: 405 - x_405 = [-1.00e-05  1.21e-03], p_k = [ 0.00221 -0.00242], α_k = 0.01562
Iteration: 406 - x_406 = [2.00e-05 1.17e-03], p_k = [-0.0047  -0.00235], α_k = 0.00781
Iteration: 407 - x_407 = [-1.00e-05  1.16e-03], p_k = [ 0.00264 -0.00231], α_k = 0.01562
Iteration: 408 - x_408 = [3.00e-05 1.12e-03], p_k = [-0.00562 -0.00224], α_k = 0.00781
Iteration: 409 - x_409 = [-2.0e-05  1.1e-03], p_k = [ 0.00316 -0.0022 ], α_k = 0.00781
Iteration: 410 - x_410 = [1.00e-05 1.08e-03], p_k = [-0.00178 -0.00217], α_k = 0.01562
Iteration: 411 - x_411 = [-2.00e-05  1.05e-03], p_k = [ 0.00378 -0.0021 ], α_k = 0.00781
Iteration: 412 - x_412 = [1.00e-05 1.03e-03], p_k = [-0.00212 -0.00207], α_k = 0.01562
Iteration: 413 - x_413 = [-2.e-05  1.e-03], p_k = [ 0.00451 -0.002  ], α_k = 0.00781
Iteration: 414 - x_414 = [1.0e-05 9.9e-04], p_k = [-0.00254 -0.00197], α_k = 0.01562
Iteration: 415 - x_415 = [-3.0e-05  9.6e-04], p_k = [ 0.0054  -0.00191], α_k = 0.00781
Iteration: 416 - x_416 = [2.0e-05 9.4e-04], p_k = [-0.00304 -0.00188], α_k = 0.00781
Iteration: 417 - x_417 = [-1.0e-05  9.3e-04], p_k = [ 0.00171 -0.00185], α_k = 0.01562
Iteration: 418 - x_418 = [2.e-05 9.e-04], p_k = [-0.00363 -0.00179], α_k = 0.00781
Iteration: 419 - x_419 = [-1.0e-05  8.8e-04], p_k = [ 0.00204 -0.00177], α_k = 0.01562
Iteration: 420 - x_420 = [2.0e-05 8.6e-04], p_k = [-0.00434 -0.00171], α_k = 0.00781
Iteration: 421 - x_421 = [-1.0e-05  8.4e-04], p_k = [ 0.00244 -0.00168], α_k = 0.00781
Iteration: 422 - x_422 = [1.0e-05 8.3e-04], p_k = [-0.00137 -0.00166], α_k = 0.01562
Iteration: 423 - x_423 = [-1.e-05  8.e-04], p_k = [ 0.00292 -0.00161], α_k = 0.00781
Iteration: 424 - x_424 = [1.0e-05 7.9e-04], p_k = [-0.00164 -0.00158], α_k = 0.01562
Iteration: 425 - x_425 = [-2.0e-05  7.7e-04], p_k = [ 0.00349 -0.00153], α_k = 0.00781
Iteration: 426 - x_426 = [1.0e-05 7.5e-04], p_k = [-0.00196 -0.00151], α_k = 0.01562
Iteration: 427 - x_427 = [-2.0e-05  7.3e-04], p_k = [ 0.00417 -0.00146], α_k = 0.00781
Iteration: 428 - x_428 = [1.0e-05 7.2e-04], p_k = [-0.00234 -0.00144], α_k = 0.00781
Iteration: 429 - x_429 = [-1.0e-05  7.1e-04], p_k = [ 0.00132 -0.00142], α_k = 0.01562
Iteration: 430 - x_430 = [1.0e-05 6.9e-04], p_k = [-0.0028  -0.00137], α_k = 0.00781
Iteration: 431 - x_431 = [-1.0e-05  6.7e-04], p_k = [ 0.00158 -0.00135], α_k = 0.01562
Iteration: 432 - x_432 = [2.0e-05 6.5e-04], p_k = [-0.00335 -0.00131], α_k = 0.00781
Iteration: 433 - x_433 = [-1.0e-05  6.4e-04], p_k = [ 0.00188 -0.00129], α_k = 0.00781
Iteration: 434 - x_434 = [1.0e-05 6.3e-04], p_k = [-0.00106 -0.00127], α_k = 0.01562
Iteration: 435 - x_435 = [-1.0e-05  6.1e-04], p_k = [ 0.00225 -0.00123], α_k = 0.00781
Iteration: 436 - x_436 = [1.e-05 6.e-04], p_k = [-0.00127 -0.00121], α_k = 0.01562
Iteration: 437 - x_437 = [-1.0e-05  5.9e-04], p_k = [ 0.00269 -0.00117], α_k = 0.00781
Iteration: 438 - x_438 = [1.0e-05 5.8e-04], p_k = [-0.00151 -0.00115], α_k = 0.01562
Iteration: 439 - x_439 = [-2.0e-05  5.6e-04], p_k = [ 0.00322 -0.00112], α_k = 0.00781
Iteration: 440 - x_440 = [1.0e-05 5.5e-04], p_k = [-0.00181 -0.0011 ], α_k = 0.00781
Iteration: 441 - x_441 = [-1.0e-05  5.4e-04], p_k = [ 0.00102 -0.00108], α_k = 0.01562
Iteration: 442 - x_442 = [1.0e-05 5.2e-04], p_k = [-0.00216 -0.00105], α_k = 0.00781
Iteration: 443 - x_443 = [-1.0e-05  5.2e-04], p_k = [ 0.00122 -0.00103], α_k = 0.01562
Iteration: 444 - x_444 = [1.e-05 5.e-04], p_k = [-0.00258 -0.001  ], α_k = 0.00781
Iteration: 445 - x_445 = [-1.0e-05  4.9e-04], p_k = [ 0.00145 -0.00098], α_k = 0.00781
Iteration: 446 - x_446 = [0.      0.00048], p_k = [-0.00082 -0.00097], α_k = 0.01562
Iteration: 447 - x_447 = [-1.0e-05  4.7e-04], p_k = [ 0.00174 -0.00094], α_k = 0.00781
Iteration: 448 - x_448 = [0.      0.00046], p_k = [-0.00098 -0.00092], α_k = 0.01562
Iteration: 449 - x_449 = [-1.0e-05  4.5e-04], p_k = [ 0.00208 -0.00089], α_k = 0.00781
Iteration: 450 - x_450 = [1.0e-05 4.4e-04], p_k = [-0.00117 -0.00088], α_k = 0.00781
Iteration: 451 - x_451 = [-0.       0.00043], p_k = [ 0.00066 -0.00087], α_k = 0.01562

Iteration: 452 - x_452 = [1.0e-05 4.2e-04], p_k = [-0.0014  -0.00084], α_k = 0.00781
Iteration: 453 - x_453 = [-0.       0.00041], p_k = [ 0.00079 -0.00083], α_k = 0.01562
Iteration: 454 - x_454 = [1.e-05 4.e-04], p_k = [-0.00167 -0.0008 ], α_k = 0.00781
Iteration: 455 - x_455 = [-0.       0.00039], p_k = [ 0.00094 -0.00079], α_k = 0.01562
Iteration: 456 - x_456 = [1.0e-05 3.8e-04], p_k = [-0.002   -0.00076], α_k = 0.00781
Iteration: 457 - x_457 = [-1.0e-05  3.8e-04], p_k = [ 0.00112 -0.00075], α_k = 0.00781
Iteration: 458 - x_458 = [0.      0.00037], p_k = [-0.00063 -0.00074], α_k = 0.01562
Iteration: 459 - x_459 = [-1.0e-05  3.6e-04], p_k = [ 0.00134 -0.00072], α_k = 0.00781
Iteration: 460 - x_460 = [0.      0.00035], p_k = [-0.00075 -0.00071], α_k = 0.01562
Iteration: 461 - x_461 = [-1.0e-05  3.4e-04], p_k = [ 0.0016  -0.00068], α_k = 0.00781
Iteration: 462 - x_462 = [0.      0.00034], p_k = [-0.0009  -0.00067], α_k = 0.00781
Iteration: 463 - x_463 = [-0.       0.00033], p_k = [ 0.00051 -0.00066], α_k = 0.01562
Iteration: 464 - x_464 = [1.0e-05 3.2e-04], p_k = [-0.00108 -0.00064], α_k = 0.00781
Iteration: 465 - x_465 = [-0.       0.00032], p_k = [ 0.00061 -0.00063], α_k = 0.01562
Iteration: 466 - x_466 = [1.0e-05 3.1e-04], p_k = [-0.00129 -0.00061], α_k = 0.00781
Iteration: 467 - x_467 = [-0.      0.0003], p_k = [ 0.00073 -0.0006 ], α_k = 0.01562
Iteration: 468 - x_468 = [1.0e-05 2.9e-04], p_k = [-0.00154 -0.00058], α_k = 0.00781
Iteration: 469 - x_469 = [-0.       0.00029], p_k = [ 0.00087 -0.00057], α_k = 0.00781
Iteration: 470 - x_470 = [0.      0.00028], p_k = [-0.00049 -0.00057], α_k = 0.01562
Iteration: 471 - x_471 = [-1.0e-05  2.7e-04], p_k = [ 0.00104 -0.00055], α_k = 0.00781
Iteration: 472 - x_472 = [0.      0.00027], p_k = [-0.00058 -0.00054], α_k = 0.01562
Iteration: 473 - x_473 = [-1.0e-05  2.6e-04], p_k = [ 0.00124 -0.00052], α_k = 0.00781
Iteration: 474 - x_474 = [0.      0.00026], p_k = [-0.0007  -0.00051], α_k = 0.00781
Iteration: 475 - x_475 = [-0.       0.00025], p_k = [ 0.00039 -0.00051], α_k = 0.01562
Iteration: 476 - x_476 = [0.      0.00025], p_k = [-0.00083 -0.00049], α_k = 0.00781
Iteration: 477 - x_477 = [-0.       0.00024], p_k = [ 0.00047 -0.00048], α_k = 0.01562
Iteration: 478 - x_478 = [0.      0.00023], p_k = [-0.001   -0.00047], α_k = 0.00781
Iteration: 479 - x_479 = [-0.       0.00023], p_k = [ 0.00056 -0.00046], α_k = 0.01562
Iteration: 480 - x_480 = [1.0e-05 2.2e-04], p_k = [-0.00119 -0.00045], α_k = 0.00781
Iteration: 481 - x_481 = [-0.       0.00022], p_k = [ 0.00067 -0.00044], α_k = 0.00781
Iteration: 482 - x_482 = [0.      0.00022], p_k = [-0.00038 -0.00043], α_k = 0.01562
Iteration: 483 - x_483 = [-0.       0.00021], p_k = [ 0.0008  -0.00042], α_k = 0.00781
Iteration: 484 - x_484 = [0.      0.00021], p_k = [-0.00045 -0.00041], α_k = 0.01562
Iteration: 485 - x_485 = [-0.      0.0002], p_k = [ 0.00096 -0.0004 ], α_k = 0.00781
Iteration: 486 - x_486 = [0.     0.0002], p_k = [-0.00054 -0.00039], α_k = 0.00781
Iteration: 487 - x_487 = [-0.       0.00019], p_k = [ 0.0003  -0.00039], α_k = 0.01562
Iteration: 488 - x_488 = [0.      0.00019], p_k = [-0.00064 -0.00037], α_k = 0.00781
Iteration: 489 - x_489 = [-0.       0.00018], p_k = [ 0.00036 -0.00037], α_k = 0.01562
Iteration: 490 - x_490 = [0.      0.00018], p_k = [-0.00077 -0.00036], α_k = 0.00781
Iteration: 491 - x_491 = [-0.       0.00018], p_k = [ 0.00043 -0.00035], α_k = 0.01562
Iteration: 492 - x_492 = [0.      0.00017], p_k = [-0.00092 -0.00034], α_k = 0.00781
Iteration: 493 - x_493 = [-0.       0.00017], p_k = [ 0.00052 -0.00034], α_k = 0.00781
Iteration: 494 - x_494 = [0.      0.00017], p_k = [-0.00029 -0.00033], α_k = 0.01562
Iteration: 495 - x_495 = [-0.       0.00016], p_k = [ 0.00062 -0.00032], α_k = 0.00781
Iteration: 496 - x_496 = [0.      0.00016], p_k = [-0.00035 -0.00031], α_k = 0.01562
Iteration: 497 - x_497 = [-0.       0.00015], p_k = [ 0.00074 -0.0003 ], α_k = 0.00781
Iteration: 498 - x_498 = [0.      0.00015], p_k = [-0.00042 -0.0003 ], α_k = 0.00781
Iteration: 499 - x_499 = [-0.       0.00015], p_k = [ 0.00023 -0.0003 ], α_k = 0.01562
Iteration: 500 - x_500 = [0.      0.00014], p_k = [-0.0005  -0.00029], α_k = 0.00781
Iteration: 501 - x_501 = [-0.       0.00014], p_k = [ 0.00028 -0.00028], α_k = 0.01562
Iteration: 502 - x_502 = [0.      0.00014], p_k = [-0.00059 -0.00027], α_k = 0.00781
Iteration: 503 - x_503 = [-0.       0.00013], p_k = [ 0.00033 -0.00027], α_k = 0.01562
Iteration: 504 - x_504 = [0.      0.00013], p_k = [-0.00071 -0.00026], α_k = 0.00781
Iteration: 505 - x_505 = [-0.       0.00013], p_k = [ 0.0004  -0.00026], α_k = 0.00781
Iteration: 506 - x_506 = [0.      0.00013], p_k = [-0.00022 -0.00025], α_k = 0.01562
Iteration: 507 - x_507 = [-0.       0.00012], p_k = [ 0.00048 -0.00024], α_k = 0.00781
Iteration: 508 - x_508 = [0.      0.00012], p_k = [-0.00027 -0.00024], α_k = 0.01562
Iteration: 509 - x_509 = [-0.       0.00012], p_k = [ 0.00057 -0.00023], α_k = 0.00781
Iteration: 510 - x_510 = [0.      0.00011], p_k = [-0.00032 -0.00023], α_k = 0.00781
Iteration: 511 - x_511 = [-0.       0.00011], p_k = [ 0.00018 -0.00023], α_k = 0.01562
Iteration: 512 - x_512 = [0.      0.00011], p_k = [-0.00038 -0.00022], α_k = 0.00781
Iteration: 513 - x_513 = [-0.       0.00011], p_k = [ 0.00022 -0.00022], α_k = 0.01562
Iteration: 514 - x_514 = [0.     0.0001], p_k = [-0.00046 -0.00021], α_k = 0.00781
Iteration: 515 - x_515 = [-0.      0.0001], p_k = [ 0.00026 -0.00021], α_k = 0.01562
Iteration: 516 - x_516 = [0.     0.0001], p_k = [-0.00055 -0.0002 ], α_k = 0.00781
Iteration: 517 - x_517 = [-0.      0.0001], p_k = [ 0.00031 -0.0002 ], α_k = 0.00781
Iteration: 518 - x_518 = [0.     0.0001], p_k = [-0.00017 -0.00019], α_k = 0.01562
Iteration: 519 - x_519 = [-0.e+00  9.e-05], p_k = [ 0.00037 -0.00019], α_k = 0.00781
Iteration: 520 - x_520 = [0.e+00 9.e-05], p_k = [-0.00021 -0.00018], α_k = 0.01562
Iteration: 521 - x_521 = [-0.e+00  9.e-05], p_k = [ 0.00044 -0.00018], α_k = 0.00781
Iteration: 522 - x_522 = [0.e+00 9.e-05], p_k = [-0.00025 -0.00018], α_k = 0.00781
Iteration: 523 - x_523 = [-0.e+00  9.e-05], p_k = [ 0.00014 -0.00017], α_k = 0.01562
Iteration: 524 - x_524 = [0.e+00 8.e-05], p_k = [-0.0003  -0.00017], α_k = 0.00781
Iteration: 525 - x_525 = [-0.e+00  8.e-05], p_k = [ 0.00017 -0.00016], α_k = 0.01562
Iteration: 526 - x_526 = [0.e+00 8.e-05], p_k = [-0.00035 -0.00016], α_k = 0.00781
Iteration: 527 - x_527 = [-0.e+00  8.e-05], p_k = [ 0.0002  -0.00016], α_k = 0.01562
Iteration: 528 - x_528 = [0.e+00 8.e-05], p_k = [-0.00042 -0.00015], α_k = 0.00781
Iteration: 529 - x_529 = [-0.e+00  7.e-05], p_k = [ 0.00024 -0.00015], α_k = 0.00781
Iteration: 530 - x_530 = [0.e+00 7.e-05], p_k = [-0.00013 -0.00015], α_k = 0.01562
Iteration: 531 - x_531 = [-0.e+00  7.e-05], p_k = [ 0.00028 -0.00014], α_k = 0.00781
Iteration: 532 - x_532 = [0.e+00 7.e-05], p_k = [-0.00016 -0.00014], α_k = 0.01562
Iteration: 533 - x_533 = [-0.e+00  7.e-05], p_k = [ 0.00034 -0.00014], α_k = 0.00781
Iteration: 534 - x_534 = [0.e+00 7.e-05], p_k = [-0.00019 -0.00013], α_k = 0.00781
Iteration: 535 - x_535 = [-0.e+00  7.e-05], p_k = [ 0.00011 -0.00013], α_k = 0.01562
Iteration: 536 - x_536 = [0.e+00 6.e-05], p_k = [-0.00023 -0.00013], α_k = 0.00781
Iteration: 537 - x_537 = [-0.e+00  6.e-05], p_k = [ 0.00013 -0.00013], α_k = 0.01562
Iteration: 538 - x_538 = [0.e+00 6.e-05], p_k = [-0.00027 -0.00012], α_k = 0.00781
Iteration: 539 - x_539 = [-0.e+00  6.e-05], p_k = [ 0.00015 -0.00012], α_k = 0.01562
Iteration: 540 - x_540 = [0.e+00 6.e-05], p_k = [-0.00033 -0.00012], α_k = 0.00781
Iteration: 541 - x_541 = [-0.e+00  6.e-05], p_k = [ 0.00018 -0.00011], α_k = 0.00781
Iteration: 542 - x_542 = [0.e+00 6.e-05], p_k = [-0.0001  -0.00011], α_k = 0.01562
Iteration: 543 - x_543 = [-0.e+00  5.e-05], p_k = [ 0.00022 -0.00011], α_k = 0.00781
Iteration: 544 - x_544 = [0.e+00 5.e-05], p_k = [-0.00012 -0.00011], α_k = 0.01562
Iteration: 545 - x_545 = [-0.e+00  5.e-05], p_k = [ 0.00026 -0.0001 ], α_k = 0.00781
Iteration: 546 - x_546 = [0.e+00 5.e-05], p_k = [-0.00015 -0.0001 ], α_k = 0.00781
Iteration: 547 - x_547 = [-0.e+00  5.e-05], p_k = [ 8.e-05 -1.e-04], α_k = 0.01562
Iteration: 548 - x_548 = [0.e+00 5.e-05], p_k = [-0.00018 -0.0001 ], α_k = 0.00781
Iteration: 549 - x_549 = [-0.e+00  5.e-05], p_k = [ 0.0001 -0.0001], α_k = 0.01562
Iteration: 550 - x_550 = [0.e+00 5.e-05], p_k = [-2.1e-04 -9.0e-05], α_k = 0.00781
Iteration: 551 - x_551 = [-0.e+00  5.e-05], p_k = [ 1.2e-04 -9.0e-05], α_k = 0.01562
Iteration: 552 - x_552 = [0.e+00 4.e-05], p_k = [-2.5e-04 -9.0e-05], α_k = 0.00781
Iteration: 553 - x_553 = [-0.e+00  4.e-05], p_k = [ 1.4e-04 -9.0e-05], α_k = 0.00781
Iteration: 554 - x_554 = [0.e+00 4.e-05], p_k = [-8.e-05 -9.e-05], α_k = 0.01562
Iteration: 555 - x_555 = [-0.e+00  4.e-05], p_k = [ 1.7e-04 -8.0e-05], α_k = 0.00781
Iteration: 556 - x_556 = [0.e+00 4.e-05], p_k = [-1.e-04 -8.e-05], α_k = 0.01562
Iteration: 557 - x_557 = [-0.e+00  4.e-05], p_k = [ 2.e-04 -8.e-05], α_k = 0.00781
Iteration: 558 - x_558 = [0.e+00 4.e-05], p_k = [-1.1e-04 -8.0e-05], α_k = 0.00781
Iteration: 559 - x_559 = [-0.e+00  4.e-05], p_k = [ 6.e-05 -8.e-05], α_k = 0.01562
Iteration: 560 - x_560 = [0.e+00 4.e-05], p_k = [-1.4e-04 -7.0e-05], α_k = 0.00781
Iteration: 561 - x_561 = [-0.e+00  4.e-05], p_k = [ 8.e-05 -7.e-05], α_k = 0.01562
Iteration: 562 - x_562 = [0.e+00 4.e-05], p_k = [-1.6e-04 -7.0e-05], α_k = 0.00781
Iteration: 563 - x_563 = [-0.e+00  4.e-05], p_k = [ 9.e-05 -7.e-05], α_k = 0.01562
Iteration: 564 - x_564 = [0.e+00 3.e-05], p_k = [-1.9e-04 -7.0e-05], α_k = 0.00781
Iteration: 565 - x_565 = [-0.e+00  3.e-05], p_k = [ 1.1e-04 -7.0e-05], α_k = 0.00781
Iteration: 566 - x_566 = [0.e+00 3.e-05], p_k = [-6.e-05 -7.e-05], α_k = 0.01562
Iteration: 567 - x_567 = [-0.e+00  3.e-05], p_k = [ 1.3e-04 -6.0e-05], α_k = 0.00781
Iteration: 568 - x_568 = [0.e+00 3.e-05], p_k = [-7.e-05 -6.e-05], α_k = 0.01562
Iteration: 569 - x_569 = [-0.e+00  3.e-05], p_k = [ 1.6e-04 -6.0e-05], α_k = 0.00781
Iteration: 570 - x_570 = [0.e+00 3.e-05], p_k = [-9.e-05 -6.e-05], α_k = 0.00781
Iteration: 571 - x_571 = [-0.e+00  3.e-05], p_k = [ 5.e-05 -6.e-05], α_k = 0.01562
Iteration: 572 - x_572 = [0.e+00 3.e-05], p_k = [-1.1e-04 -6.0e-05], α_k = 0.00781
Iteration: 573 - x_573 = [-0.e+00  3.e-05], p_k = [ 6.e-05 -6.e-05], α_k = 0.01562
Iteration: 574 - x_574 = [0.e+00 3.e-05], p_k = [-1.3e-04 -5.0e-05], α_k = 0.00781
Iteration: 575 - x_575 = [-0.e+00  3.e-05], p_k = [ 7.e-05 -5.e-05], α_k = 0.01562
Iteration: 576 - x_576 = [0.e+00 3.e-05], p_k = [-1.5e-04 -5.0e-05], α_k = 0.00781
Iteration: 577 - x_577 = [-0.e+00  3.e-05], p_k = [ 8.e-05 -5.e-05], α_k = 0.00781
Iteration: 578 - x_578 = [0.e+00 3.e-05], p_k = [-5.e-05 -5.e-05], α_k = 0.01562
Iteration: 579 - x_579 = [-0.e+00  2.e-05], p_k = [ 1.e-04 -5.e-05], α_k = 0.00781
Iteration: 580 - x_580 = [0.e+00 2.e-05], p_k = [-6.e-05 -5.e-05], α_k = 0.01562
Iteration: 581 - x_581 = [-0.e+00  2.e-05], p_k = [ 1.2e-04 -5.0e-05], α_k = 0.00781
Iteration: 582 - x_582 = [0.e+00 2.e-05], p_k = [-7.e-05 -5.e-05], α_k = 0.00781
Iteration: 583 - x_583 = [-0.e+00  2.e-05], p_k = [ 4.e-05 -4.e-05], α_k = 0.01562
Iteration: 584 - x_584 = [0.e+00 2.e-05], p_k = [-8.e-05 -4.e-05], α_k = 0.00781
Iteration: 585 - x_585 = [-0.e+00  2.e-05], p_k = [ 5.e-05 -4.e-05], α_k = 0.01562
Iteration: 586 - x_586 = [0.e+00 2.e-05], p_k = [-1.e-04 -4.e-05], α_k = 0.00781
Iteration: 587 - x_587 = [-0.e+00  2.e-05], p_k = [ 5.e-05 -4.e-05], α_k = 0.00781

Iteration: 588 - x_588 = [0.e+00 2.e-05], p_k = [-3.e-05 -4.e-05], α_k = 0.01562
Iteration: 589 - x_589 = [-0.e+00  2.e-05], p_k = [ 7.e-05 -4.e-05], α_k = 0.00781
Iteration: 590 - x_590 = [0.e+00 2.e-05], p_k = [-4.e-05 -4.e-05], α_k = 0.01562
Iteration: 591 - x_591 = [-0.e+00  2.e-05], p_k = [ 8.e-05 -4.e-05], α_k = 0.00781
Iteration: 592 - x_592 = [0.e+00 2.e-05], p_k = [-4.e-05 -4.e-05], α_k = 0.01562
Iteration: 593 - x_593 = [-0.e+00  2.e-05], p_k = [ 9.e-05 -4.e-05], α_k = 0.00781
Iteration: 594 - x_594 = [0.e+00 2.e-05], p_k = [-5.e-05 -3.e-05], α_k = 0.00781
Iteration: 595 - x_595 = [-0.e+00  2.e-05], p_k = [ 3.e-05 -3.e-05], α_k = 0.01562
Iteration: 596 - x_596 = [0.e+00 2.e-05], p_k = [-6.e-05 -3.e-05], α_k = 0.00781
Iteration: 597 - x_597 = [-0.e+00  2.e-05], p_k = [ 4.e-05 -3.e-05], α_k = 0.01562
Iteration: 598 - x_598 = [0.e+00 2.e-05], p_k = [-7.e-05 -3.e-05], α_k = 0.00781
Iteration: 599 - x_599 = [-0.e+00  2.e-05], p_k = [ 4.e-05 -3.e-05], α_k = 0.00781
Iteration: 600 - x_600 = [0.e+00 2.e-05], p_k = [-2.e-05 -3.e-05], α_k = 0.01562
Iteration: 601 - x_601 = [-0.e+00  1.e-05], p_k = [ 5.e-05 -3.e-05], α_k = 0.00781
Iteration: 602 - x_602 = [0.e+00 1.e-05], p_k = [-3.e-05 -3.e-05], α_k = 0.01562
Iteration: 603 - x_603 = [-0.e+00  1.e-05], p_k = [ 6.e-05 -3.e-05], α_k = 0.00781
Iteration: 604 - x_604 = [0.e+00 1.e-05], p_k = [-3.e-05 -3.e-05], α_k = 0.01562
Iteration: 605 - x_605 = [-0.e+00  1.e-05], p_k = [ 7.e-05 -3.e-05], α_k = 0.00781
Iteration: 606 - x_606 = [0.e+00 1.e-05], p_k = [-4.e-05 -3.e-05], α_k = 0.00781
Iteration: 607 - x_607 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -3.e-05], α_k = 0.01562
Iteration: 608 - x_608 = [0.e+00 1.e-05], p_k = [-5.e-05 -3.e-05], α_k = 0.00781
Iteration: 609 - x_609 = [-0.e+00  1.e-05], p_k = [ 3.e-05 -3.e-05], α_k = 0.01562
Iteration: 610 - x_610 = [0.e+00 1.e-05], p_k = [-6.e-05 -2.e-05], α_k = 0.00781
Iteration: 611 - x_611 = [-0.e+00  1.e-05], p_k = [ 3.e-05 -2.e-05], α_k = 0.00781
Iteration: 612 - x_612 = [0.e+00 1.e-05], p_k = [-2.e-05 -2.e-05], α_k = 0.01562
Iteration: 613 - x_613 = [-0.e+00  1.e-05], p_k = [ 4.e-05 -2.e-05], α_k = 0.00781
Iteration: 614 - x_614 = [0.e+00 1.e-05], p_k = [-2.e-05 -2.e-05], α_k = 0.01562
Iteration: 615 - x_615 = [-0.e+00  1.e-05], p_k = [ 5.e-05 -2.e-05], α_k = 0.00781
Iteration: 616 - x_616 = [0.e+00 1.e-05], p_k = [-3.e-05 -2.e-05], α_k = 0.01562
Iteration: 617 - x_617 = [-0.e+00  1.e-05], p_k = [ 6.e-05 -2.e-05], α_k = 0.00781
Iteration: 618 - x_618 = [0.e+00 1.e-05], p_k = [-3.e-05 -2.e-05], α_k = 0.00781
Iteration: 619 - x_619 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -2.e-05], α_k = 0.01562
Iteration: 620 - x_620 = [0.e+00 1.e-05], p_k = [-4.e-05 -2.e-05], α_k = 0.00781
Iteration: 621 - x_621 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -2.e-05], α_k = 0.01562
Iteration: 622 - x_622 = [0.e+00 1.e-05], p_k = [-4.e-05 -2.e-05], α_k = 0.00781
Iteration: 623 - x_623 = [-0.e+00  1.e-05], p_k = [ 3.e-05 -2.e-05], α_k = 0.00781
Iteration: 624 - x_624 = [0.e+00 1.e-05], p_k = [-1.e-05 -2.e-05], α_k = 0.01562
Iteration: 625 - x_625 = [-0.e+00  1.e-05], p_k = [ 3.e-05 -2.e-05], α_k = 0.00781
Iteration: 626 - x_626 = [0.e+00 1.e-05], p_k = [-2.e-05 -2.e-05], α_k = 0.01562
Iteration: 627 - x_627 = [-0.e+00  1.e-05], p_k = [ 4.e-05 -2.e-05], α_k = 0.00781
Iteration: 628 - x_628 = [0.e+00 1.e-05], p_k = [-2.e-05 -2.e-05], α_k = 0.01562
Iteration: 629 - x_629 = [-0.e+00  1.e-05], p_k = [ 4.e-05 -2.e-05], α_k = 0.00781
Iteration: 630 - x_630 = [0.e+00 1.e-05], p_k = [-2.e-05 -2.e-05], α_k = 0.00781
Iteration: 631 - x_631 = [-0.e+00  1.e-05], p_k = [ 1.e-05 -2.e-05], α_k = 0.01562
Iteration: 632 - x_632 = [0.e+00 1.e-05], p_k = [-3.e-05 -1.e-05], α_k = 0.00781
Iteration: 633 - x_633 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -1.e-05], α_k = 0.01562
Iteration: 634 - x_634 = [0.e+00 1.e-05], p_k = [-3.e-05 -1.e-05], α_k = 0.00781
Iteration: 635 - x_635 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 636 - x_636 = [0.e+00 1.e-05], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 637 - x_637 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 638 - x_638 = [0.e+00 1.e-05], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 639 - x_639 = [-0.e+00  1.e-05], p_k = [ 3.e-05 -1.e-05], α_k = 0.00781
Iteration: 640 - x_640 = [0.e+00 1.e-05], p_k = [-2.e-05 -1.e-05], α_k = 0.01562
Iteration: 641 - x_641 = [-0.e+00  1.e-05], p_k = [ 3.e-05 -1.e-05], α_k = 0.00781
Iteration: 642 - x_642 = [0.e+00 1.e-05], p_k = [-2.e-05 -1.e-05], α_k = 0.00781
Iteration: 643 - x_643 = [-0.e+00  1.e-05], p_k = [ 1.e-05 -1.e-05], α_k = 0.01562
Iteration: 644 - x_644 = [0.e+00 1.e-05], p_k = [-2.e-05 -1.e-05], α_k = 0.00781
Iteration: 645 - x_645 = [-0.e+00  1.e-05], p_k = [ 1.e-05 -1.e-05], α_k = 0.01562
Iteration: 646 - x_646 = [0.e+00 1.e-05], p_k = [-3.e-05 -1.e-05], α_k = 0.00781
Iteration: 647 - x_647 = [-0.e+00  1.e-05], p_k = [ 1.e-05 -1.e-05], α_k = 0.00781
Iteration: 648 - x_648 = [0.e+00 1.e-05], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 649 - x_649 = [-0.e+00  1.e-05], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 650 - x_650 = [0.e+00 1.e-05], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 651 - x_651 = [-0.  0.], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 652 - x_652 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 653 - x_653 = [-0.  0.], p_k = [ 3.e-05 -1.e-05], α_k = 0.00781
Iteration: 654 - x_654 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.00781
Iteration: 655 - x_655 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.01562
Iteration: 656 - x_656 = [0. 0.], p_k = [-2.e-05 -1.e-05], α_k = 0.00781
Iteration: 657 - x_657 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.01562
Iteration: 658 - x_658 = [0. 0.], p_k = [-2.e-05 -1.e-05], α_k = 0.00781
Iteration: 659 - x_659 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.00781
Iteration: 660 - x_660 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 661 - x_661 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.00781
Iteration: 662 - x_662 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 663 - x_663 = [-0.  0.], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 664 - x_664 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 665 - x_665 = [-0.  0.], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 666 - x_666 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.00781
Iteration: 667 - x_667 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.01562
Iteration: 668 - x_668 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.00781
Iteration: 669 - x_669 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.01562
Iteration: 670 - x_670 = [0. 0.], p_k = [-2.e-05 -1.e-05], α_k = 0.00781
Iteration: 671 - x_671 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.00781
Iteration: 672 - x_672 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 673 - x_673 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.00781
Iteration: 674 - x_674 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 675 - x_675 = [-0.  0.], p_k = [ 1.e-05 -1.e-05], α_k = 0.00781
Iteration: 676 - x_676 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.01562
Iteration: 677 - x_677 = [-0.  0.], p_k = [ 2.e-05 -1.e-05], α_k = 0.00781
Iteration: 678 - x_678 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.00781
Iteration: 679 - x_679 = [-0.  0.], p_k = [ 0.e+00 -1.e-05], α_k = 0.01562
Iteration: 680 - x_680 = [0. 0.], p_k = [-1.e-05 -1.e-05], α_k = 0.00781
Iteration: 681 - x_681 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.01562
Iteration: 682 - x_682 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 683 - x_683 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 684 - x_684 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 685 - x_685 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 686 - x_686 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 687 - x_687 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 688 - x_688 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.01562
Iteration: 689 - x_689 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 690 - x_690 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 691 - x_691 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 692 - x_692 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 693 - x_693 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 694 - x_694 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 695 - x_695 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 696 - x_696 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 697 - x_697 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 698 - x_698 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 699 - x_699 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 700 - x_700 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 701 - x_701 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 702 - x_702 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 703 - x_703 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 704 - x_704 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 705 - x_705 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 706 - x_706 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 707 - x_707 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 708 - x_708 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 709 - x_709 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 710 - x_710 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 711 - x_711 = [-0.  0.], p_k = [ 1.e-05 -0.e+00], α_k = 0.00781
Iteration: 712 - x_712 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 713 - x_713 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 714 - x_714 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 715 - x_715 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 716 - x_716 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 717 - x_717 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 718 - x_718 = [0. 0.], p_k = [-1.e-05 -0.e+00], α_k = 0.00781
Iteration: 719 - x_719 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 720 - x_720 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 721 - x_721 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 722 - x_722 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 723 - x_723 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 724 - x_724 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 725 - x_725 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 726 - x_726 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 727 - x_727 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 728 - x_728 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781

Iteration: 729 - x_729 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 730 - x_730 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 731 - x_731 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 732 - x_732 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 733 - x_733 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 734 - x_734 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 735 - x_735 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 736 - x_736 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 737 - x_737 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 738 - x_738 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 739 - x_739 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 740 - x_740 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 741 - x_741 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 742 - x_742 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 743 - x_743 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 744 - x_744 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 745 - x_745 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 746 - x_746 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 747 - x_747 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 748 - x_748 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 749 - x_749 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 750 - x_750 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 751 - x_751 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 752 - x_752 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 753 - x_753 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.01562
Iteration: 754 - x_754 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Iteration: 755 - x_755 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 756 - x_756 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 757 - x_757 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 758 - x_758 = [0. 0.], p_k = [-0. -0.], α_k = 0.01562
Iteration: 759 - x_759 = [-0.  0.], p_k = [ 0. -0.], α_k = 0.00781
Iteration: 760 - x_760 = [0. 0.], p_k = [-0. -0.], α_k = 0.00781
Series diverged.
time: 532 ms

(b) Do the same with Newton’s Method.

def newton_raphson_opt(
    f, f_prime, hessian, x_0, ε=1e-15, steplength_algo=simple_steplength
):
    """This method here is exactly the same as the 
    Newton method for root finding except that f is 
    the function we're trying to find the optimum point
    for  - using the newton raphson root finding but for
    the derivative of f, and this method is applicable to
    higher dimensions
    """
    k, x_k = 0, x_0
    while True:

        # 1. Test for Convergence
        if np.allclose(f_prime(x=x_k), 0, rtol=ε):
            return x_k

        # 2. Compute a search direction
        p_k = -np.linalg.inv(hessian(x=x_k)) @ f_prime(x=x_k)

        # 3. Compute a steplength
        α_k = steplength_algo(f=f, f_prime=f_prime, x_k=x_k, p_k=p_k, μ=1e-4)

        print(
            f"Iteration: {k} - x_{k} = {np.round(x_k, 5)}, p_k = {np.round(p_k, 5)}, α_k = {np.round(α_k, 5)}, hessian = {np.round(hessian(x=x_k), 5)}"
        )

        # 4. Update the iterate and return to Step 1
        k += 1
        x_k += α_k * p_k

        # Check for divergence
        if np.allclose(x_k, x_k + α_k * p_k) and k > 1:
            print("Series diverged.")
            break

time: 2.4 ms

c = 2
print(f"Newton's Method with c={c}:")
print("=" * 30)
newton_raphson_opt(
    f=functools.partial(f, c=c),
    f_prime=functools.partial(f_prime, c=c),
    hessian=functools.partial(hessian, c=c),
    x_0=np.array([10.0, 10.0]),
    ε=1e-15,
)

Newton's Method with c=2:
==============================
Iteration: 0 - x_0 = [10. 10.], p_k = [-10. -10.], α_k = 1, hessian = [[4 0]
 [0 2]]

array([0., 0.])

time: 4.5 ms

c = 10
print(f"Newton's Method with c={c}:")
print("=" * 30)
newton_raphson_opt(
    f=functools.partial(f, c=c),
    f_prime=functools.partial(f_prime, c=c),
    hessian=functools.partial(hessian, c=c),
    x_0=np.array([10.0, 10.0]),
    ε=1e-15,
)

Newton's Method with c=10:
==============================
Iteration: 0 - x_0 = [10. 10.], p_k = [-10. -10.], α_k = 1, hessian = [[20  0]
 [ 0  2]]

array([0., 0.])

time: 4.6 ms

c = 100
print(f"Newton's Method with c={c}:")
print("=" * 30)
newton_raphson_opt(
    f=functools.partial(f, c=c),
    f_prime=functools.partial(f_prime, c=c),
    hessian=functools.partial(hessian, c=c),
    x_0=np.array([10.0, 10.0]),
    ε=1e-15,
)

Newton's Method with c=100:
==============================
Iteration: 0 - x_0 = [10. 10.], p_k = [-10. -10.], α_k = 1, hessian = [[200   0]
 [  0   2]]

array([0., 0.])

time: 4.58 ms

Since the Hessian of the function is positive definite for \(c > 0\), Newton’s method search direction \(p_k\) jumps directly to the minimum of the function, and hence, with all 3 \(c\)’s, Newton’s Method only takes 1 iteration.

Extra Questions

1.

Show that the univariate function \(f(x) = x^{4/3}\) has a unique minimizer at \(x = 0\) but that for any nonzero initial point, the Newton sequence for minimizing \(f\) diverges.

f = lambda x: x ** (4 / 3)
x = np.linspace(0, 100, 1000)
plt.title("$f(x) = x^{4/3}$")
plt.plot(x, f(x))
plt.grid(True)
plt.show()
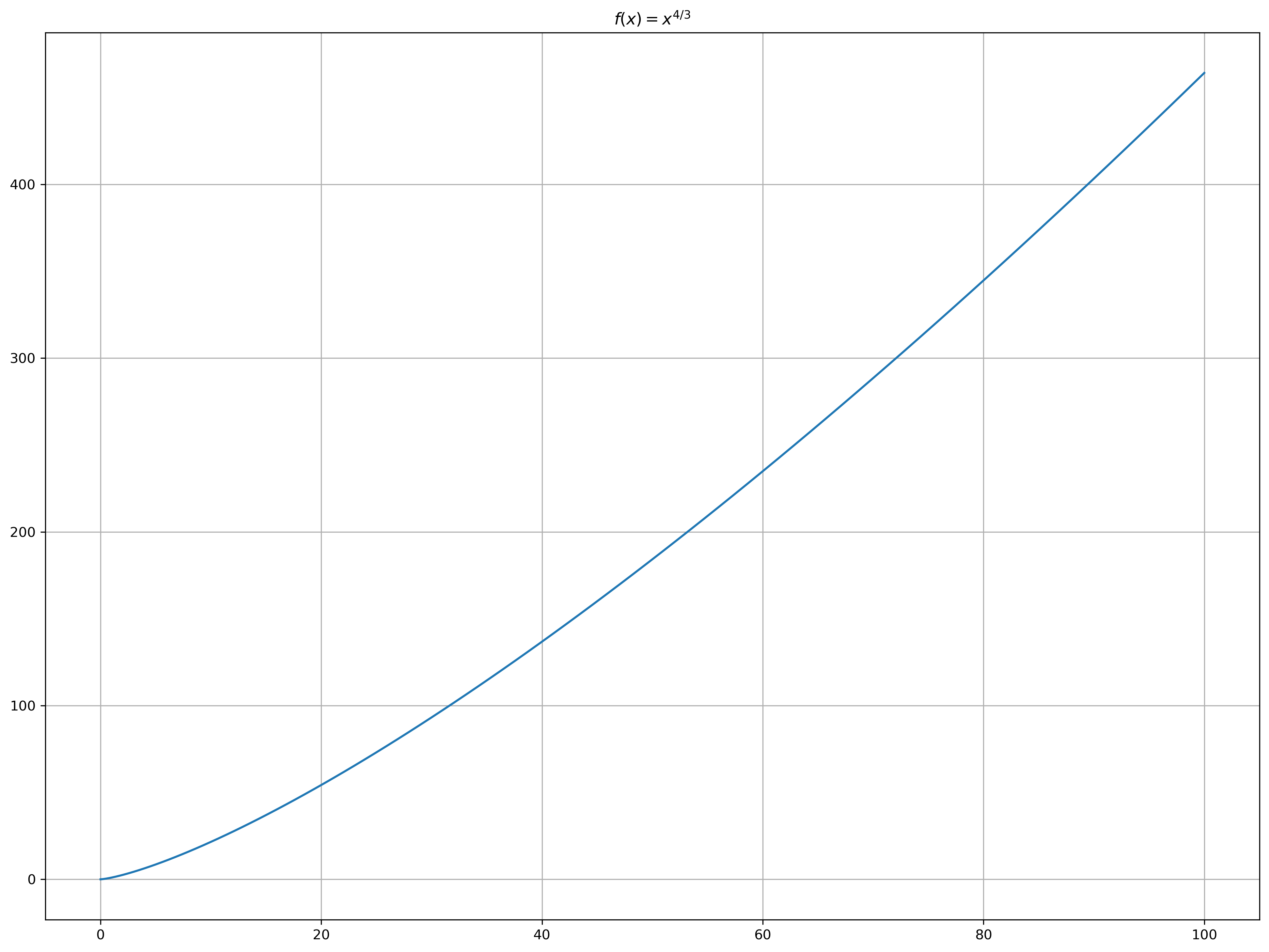
../../_images/hw4_61_0.png 
time: 1.76 s
(232)\[\begin{align} f^{\prime}(x) &= 4/3x^{1/3} \\ f^{\prime\prime}(x) &= 4/9x^{-2/3} \\ \end{align}\]

At the stationary point, \(f^\prime (x) = 0\), meaning that \(x=0\) is the stationary point. \(f^\prime (x>0) > 0\), while \(f^\prime (x<0) < 0\), meaning that \(x=0\) is a unique minimizer. \(\blacksquare\)

Proof by Contradiction:

Assuming unit steplength \(\alpha_k = 1\), and suppose \(x_0 \not= 0\) (\(x_0 > 0\) actually, since \(f(x)\) is undefined for \(x < 0\)),

Newton’s Method coordinate update step:

(233)\[\begin{align} x_{k+1} &= x_k + \alpha_k p_k \\ &= x_k + p_k \\ &= x_k - \frac{f\prime(x_k)}{f^{\prime\prime}(x_k)} \\ &= x_k -(4/9x^{-2/3}_k)(4/3x^{1/3}_k) \\ &= x_k -16/27 x^{-1/3}_k \\ \end{align}\]

Assuming \(\underset{k \rightarrow \infty}{\lim}x_k = L\) (we converge to an optimal value),

(234)\[\begin{align} L &= L -\frac{16}{27L^{1/3}} \\ 0 &= -\frac{16}{27L^{1/3}} \\ \end{align}\]

If \(L \not= 0\), the equation above is contradicting since LHS \(\rightarrow 0\), RHS \(\rightarrow -\infty\).

Hence, Newton’s Method’s coordinate update step is undefined for any value of \(x_k\), sequence diverges for any nonzero initial point. (When \(x_0 = 0\), Newton’s Method outputs the optimal \(x = x_0\) because test of convergence is before the update step). \(\blacksquare\)

2.

Compute the first two iterates of the Newton Method (with unit step) starting with \(x^0 = (0, 0)\) for minimizing the function: \(f(x_1, x_2) = 2x^4_1 + x^2_2 − 4x_1x_2 + 5x_2\). Do the same with the steepest descent method with exact line search.

def line_search(f, f_prime, x_k, p_k, μ=1e-4, η=1):
    """α = argmin_α f(xk + αpk), η=1 for exact, η small for accurate line search"""
    # 1. Set α=1.
    α = 1
    while True:
        # 2. Wolfe conditions:
        # If f(xk+αpk) ≤ f(xk)+μαgkpk, and |g(x+αpk).Tpk| ≤ η|g(xk).Tpk|, set αk=α and stop.
        if f(x_k + α * p_k) <= f(x_k) + μ * α * f_prime(x_k).T @ p_k and np.abs(
            f_prime(x_k + α * p_k).T @ p_k
        ) <= η * np.abs(f_prime(x_k).T @ p_k):
            return α
        else:
            # 3. Set α=α/2 and go to Step2.
            α /= 2

time: 1.38 ms

Gradient Vector:

(235)\[\begin{align} \nabla f(x_1, x_2) &= \begin{bmatrix} 8x^3_1 - 4x_2 \\ 2x_2 - 4x_1 + 5 \\ \end{bmatrix} \\ \end{align}\]

Hessian:

(236)\[\begin{align} \nabla f(x_1, x_2) &= \begin{bmatrix} 24x^2_1 & -4 \\ -4 & 2 \\ \end{bmatrix} \\ \end{align}\]
f = lambda x: 2 * (x[0] ** 4) + x[1] ** 2 - 4 * x[0] * x[1] + 5 * x[1]
f_prime = lambda x: np.array([8 * (x[0] ** 3) - 4 * x[1], 2 * x[1] - 4 * x[0] + 5])
hessian = lambda x: np.array([[24 * (x[0] ** 2), -4], [-4, 2]])

time: 1.36 ms

Newton’s Method with Exact Line Search (\(\eta = 1\) in Wolfe Conditions)

newton_raphson_opt(
    f=f,
    f_prime=f_prime,
    hessian=hessian,
    x_0=np.array([0.0, 0.0]),
    steplength_algo=line_search,
)

Iteration: 0 - x_0 = [0. 0.], p_k = [1.25 0.  ], α_k = 0.0, hessian = [[ 0. -4.]
 [-4.  2.]]
Iteration: 1 - x_1 = [0. 0.], p_k = [1.25 0.  ], α_k = 0.0, hessian = [[ 0. -4.]
 [-4.  2.]]
Series diverged.
time: 15.9 ms

Steepest Descent with Exact Line Search (\(\eta = 1\) in Wolfe Conditions)

steepest_descent(
    f=f, f_prime=f_prime, x_0=np.array([0.0, 0.0]), steplength_algo=line_search
)

Iteration: 0 - x_0 = [0. 0.], p_k = [-0. -5.], α_k = 0.5
Iteration: 1 - x_1 = [ 0.  -2.5], p_k = [-10.  -0.], α_k = 0.125
Iteration: 2 - x_2 = [-1.25 -2.5 ], p_k = [ 5.625 -5.   ], α_k = 0.0625
Iteration: 3 - x_3 = [-0.89844 -2.8125 ], p_k = [-5.44832 -2.96875], α_k = 0.0625
Iteration: 4 - x_4 = [-1.23896 -2.99805], p_k = [ 3.22237 -3.95974], α_k = 0.0625
Iteration: 5 - x_5 = [-1.03756 -3.24553], p_k = [-4.04641 -2.65918], α_k = 0.0625
Iteration: 6 - x_6 = [-1.29046 -3.41173], p_k = [ 3.54499 -3.33838], α_k = 0.0625
Iteration: 7 - x_7 = [-1.0689  -3.62038], p_k = [-4.7114  -2.03484], α_k = 0.0625
Iteration: 8 - x_8 = [-1.36336 -3.74756], p_k = [ 5.283   -2.95833], α_k = 0.03125
Iteration: 9 - x_9 = [-1.19827 -3.84   ], p_k = [-1.5958  -2.11306], α_k = 0.125
Iteration: 10 - x_10 = [-1.39774 -4.10414], p_k = [ 5.42945 -2.3827 ], α_k = 0.03125
Iteration: 11 - x_11 = [-1.22807 -4.1786 ], p_k = [-1.89732 -1.5551 ], α_k = 0.0625
Iteration: 12 - x_12 = [-1.34666 -4.27579], p_k = [ 2.4339  -1.83504], α_k = 0.0625
Iteration: 13 - x_13 = [-1.19454 -4.39048], p_k = [-3.92589 -0.99719], α_k = 0.03125
Iteration: 14 - x_14 = [-1.31722 -4.42164], p_k = [ 0.59718 -1.4256 ], α_k = 0.125
Iteration: 15 - x_15 = [-1.24257 -4.59984], p_k = [-3.05123 -0.77061], α_k = 0.03125
Iteration: 16 - x_16 = [-1.33792 -4.62392], p_k = [ 0.66381 -1.10385], α_k = 0.125
Iteration: 17 - x_17 = [-1.25495 -4.7619 ], p_k = [-3.23634 -0.49598], α_k = 0.03125
Iteration: 18 - x_18 = [-1.35608 -4.7774 ], p_k = [ 0.84067 -0.86953], α_k = 0.0625
Iteration: 19 - x_19 = [-1.30354 -4.83175], p_k = [-1.60697 -0.55067], α_k = 0.03125
Iteration: 20 - x_20 = [-1.35376 -4.84896], p_k = [ 0.45205 -0.71712], α_k = 0.0625
Iteration: 21 - x_21 = [-1.32551 -4.89378], p_k = [-0.94416 -0.51447], α_k = 0.0625
Iteration: 22 - x_22 = [-1.38452 -4.92593], p_k = [ 1.52793 -0.6862 ], α_k = 0.03125
Iteration: 23 - x_23 = [-1.33677 -4.94738], p_k = [-0.67961 -0.45232], α_k = 0.0625
Iteration: 24 - x_24 = [-1.37924 -4.97565], p_k = [ 1.08745 -0.56568], α_k = 0.03125
Iteration: 25 - x_25 = [-1.34526 -4.99332], p_k = [-0.49685 -0.3944 ], α_k = 0.0625
Iteration: 26 - x_26 = [-1.37631 -5.01797], p_k = [ 0.78467 -0.46931], α_k = 0.03125
Iteration: 27 - x_27 = [-1.35179 -5.03264], p_k = [-0.36901 -0.3419 ], α_k = 0.0625
Iteration: 28 - x_28 = [-1.37486 -5.05401], p_k = [ 0.57434 -0.39141], α_k = 0.03125
Iteration: 29 - x_29 = [-1.35691 -5.06624], p_k = [-0.27823 -0.29516], α_k = 0.0625
Iteration: 30 - x_30 = [-1.3743  -5.08469], p_k = [ 0.42629 -0.32782], α_k = 0.03125
Iteration: 31 - x_31 = [-1.36098 -5.09493], p_k = [-0.2127  -0.25404], α_k = 0.125
Iteration: 32 - x_32 = [-1.38756 -5.12669], p_k = [ 0.86545 -0.29688], α_k = 0.03125
Iteration: 33 - x_33 = [-1.36052 -5.13596], p_k = [-0.39717 -0.17015], α_k = 0.03125
Iteration: 34 - x_34 = [-1.37293 -5.14128], p_k = [ 0.13798 -0.20916], α_k = 0.0625
Iteration: 35 - x_35 = [-1.36431 -5.15435], p_k = [-0.30199 -0.14852], α_k = 0.03125
Iteration: 36 - x_36 = [-1.37374 -5.15899], p_k = [ 0.10395 -0.17699], α_k = 0.0625
Iteration: 37 - x_37 = [-1.36725 -5.17006], p_k = [-0.23316 -0.12888], α_k = 0.0625
Iteration: 38 - x_38 = [-1.38182 -5.17811], p_k = [ 0.3954  -0.17106], α_k = 0.03125
Iteration: 39 - x_39 = [-1.36946 -5.18346], p_k = [-0.18717 -0.11094], α_k = 0.0625
Iteration: 40 - x_40 = [-1.38116 -5.19039], p_k = [ 0.31615 -0.14387], α_k = 0.03125
Iteration: 41 - x_41 = [-1.37128 -5.19489], p_k = [-0.15092 -0.09536], α_k = 0.0625
Iteration: 42 - x_42 = [-1.38071 -5.20085], p_k = [ 0.25387 -0.12117], α_k = 0.03125
Iteration: 43 - x_43 = [-1.37278 -5.20463], p_k = [-0.12217 -0.08186], α_k = 0.0625
Iteration: 44 - x_44 = [-1.38042 -5.20975], p_k = [ 0.20464 -0.10217], α_k = 0.03125
Iteration: 45 - x_45 = [-1.37402 -5.21294], p_k = [-0.09924 -0.0702 ], α_k = 0.0625
Iteration: 46 - x_46 = [-1.38022 -5.21733], p_k = [ 0.16552 -0.08624], α_k = 0.03125
Iteration: 47 - x_47 = [-1.37505 -5.22002], p_k = [-0.08087 -0.06016], α_k = 0.0625
Iteration: 48 - x_48 = [-1.38011 -5.22378], p_k = [ 0.13429 -0.07286], α_k = 0.03125
Iteration: 49 - x_49 = [-1.37591 -5.22606], p_k = [-0.06607 -0.05152], α_k = 0.0625
Iteration: 50 - x_50 = [-1.38004 -5.22928], p_k = [ 0.10923 -0.06159], α_k = 0.03125
Iteration: 51 - x_51 = [-1.37663 -5.23121], p_k = [-0.05411 -0.04409], α_k = 0.0625
Iteration: 52 - x_52 = [-1.38001 -5.23396], p_k = [ 0.08905 -0.05211], α_k = 0.03125
Iteration: 53 - x_53 = [-1.37722 -5.23559], p_k = [-0.0444  -0.03772], α_k = 0.0625
Iteration: 54 - x_54 = [-1.38    -5.23795], p_k = [ 0.07275 -0.0441 ], α_k = 0.03125
Iteration: 55 - x_55 = [-1.37773 -5.23932], p_k = [-0.0365  -0.03225], α_k = 0.0625
Iteration: 56 - x_56 = [-1.38001 -5.24134], p_k = [ 0.05953 -0.03735], α_k = 0.03125
Iteration: 57 - x_57 = [-1.37815 -5.24251], p_k = [-0.03005 -0.02757], α_k = 0.0625
Iteration: 58 - x_58 = [-1.38002 -5.24423], p_k = [ 0.04879 -0.03164], α_k = 0.03125
Iteration: 59 - x_59 = [-1.3785  -5.24522], p_k = [-0.02478 -0.02356], α_k = 0.0625
Iteration: 60 - x_60 = [-1.38005 -5.24669], p_k = [ 0.04003 -0.02681], α_k = 0.03125
Iteration: 61 - x_61 = [-1.3788  -5.24753], p_k = [-0.02045 -0.02013], α_k = 0.0625
Iteration: 62 - x_62 = [-1.38008 -5.24879], p_k = [ 0.03289 -0.02273], α_k = 0.03125
Iteration: 63 - x_63 = [-1.37905 -5.2495 ], p_k = [-0.0169 -0.0172], α_k = 0.0625
Iteration: 64 - x_64 = [-1.3801  -5.25057], p_k = [ 0.02704 -0.01927], α_k = 0.03125
Iteration: 65 - x_65 = [-1.37926 -5.25118], p_k = [-0.01397 -0.01469], α_k = 0.0625
Iteration: 66 - x_66 = [-1.38013 -5.25209], p_k = [ 0.02225 -0.01634], α_k = 0.03125
Iteration: 67 - x_67 = [-1.37944 -5.2526 ], p_k = [-0.01156 -0.01254], α_k = 0.0625
Iteration: 68 - x_68 = [-1.38016 -5.25339], p_k = [ 0.01833 -0.01386], α_k = 0.03125
Iteration: 69 - x_69 = [-1.37959 -5.25382], p_k = [-0.00958 -0.01071], α_k = 0.0625
Iteration: 70 - x_70 = [-1.38019 -5.25449], p_k = [ 0.0151  -0.01176], α_k = 0.03125
Iteration: 71 - x_71 = [-1.37971 -5.25486], p_k = [-0.00794 -0.00914], α_k = 0.0625
Iteration: 72 - x_72 = [-1.38021 -5.25543], p_k = [ 0.01245 -0.00998], α_k = 0.03125
Iteration: 73 - x_73 = [-1.37982 -5.25574], p_k = [-0.00658 -0.0078 ], α_k = 0.0625
Iteration: 74 - x_74 = [-1.38023 -5.25623], p_k = [ 0.01027 -0.00847], α_k = 0.0625
Iteration: 75 - x_75 = [-1.37959 -5.25676], p_k = [-0.02117 -0.00485], α_k = 0.03125
Iteration: 76 - x_76 = [-1.38025 -5.25691], p_k = [ 0.00846 -0.00719], α_k = 0.0625
Iteration: 77 - x_77 = [-1.37972 -5.25736], p_k = [-0.0175  -0.00418], α_k = 0.03125
Iteration: 78 - x_78 = [-1.38027 -5.25749], p_k = [ 0.00697 -0.0061 ], α_k = 0.0625
Iteration: 79 - x_79 = [-1.37983 -5.25787], p_k = [-0.01448 -0.0036 ], α_k = 0.03125
Iteration: 80 - x_80 = [-1.38029 -5.25798], p_k = [ 0.00575 -0.00518], α_k = 0.0625
Iteration: 81 - x_81 = [-1.37993 -5.25831], p_k = [-0.01198 -0.0031 ], α_k = 0.03125
Iteration: 82 - x_82 = [-1.3803 -5.2584], p_k = [ 0.00475 -0.0044 ], α_k = 0.0625
Iteration: 83 - x_83 = [-1.38    -5.25868], p_k = [-0.00991 -0.00266], α_k = 0.03125
Iteration: 84 - x_84 = [-1.38031 -5.25876], p_k = [ 0.00392 -0.00374], α_k = 0.0625
Iteration: 85 - x_85 = [-1.38007 -5.259  ], p_k = [-0.00821 -0.00229], α_k = 0.03125
Iteration: 86 - x_86 = [-1.38033 -5.25907], p_k = [ 0.00323 -0.00317], α_k = 0.0625
Iteration: 87 - x_87 = [-1.38012 -5.25926], p_k = [-0.0068  -0.00197], α_k = 0.03125
Iteration: 88 - x_88 = [-1.38034 -5.25933], p_k = [ 0.00267 -0.00269], α_k = 0.0625
Iteration: 89 - x_89 = [-1.38017 -5.25949], p_k = [-0.00563 -0.00169], α_k = 0.03125
Iteration: 90 - x_90 = [-1.38035 -5.25955], p_k = [ 0.0022  -0.00229], α_k = 0.0625
Iteration: 91 - x_91 = [-1.38021 -5.25969], p_k = [-0.00467 -0.00145], α_k = 0.03125
Iteration: 92 - x_92 = [-1.38035 -5.25974], p_k = [ 0.00182 -0.00194], α_k = 0.0625
Iteration: 93 - x_93 = [-1.38024 -5.25986], p_k = [-0.00387 -0.00125], α_k = 0.03125
Iteration: 94 - x_94 = [-1.38036 -5.2599 ], p_k = [ 0.0015  -0.00165], α_k = 0.0625
Iteration: 95 - x_95 = [-1.38027 -5.26   ], p_k = [-0.0032  -0.00107], α_k = 0.03125
Iteration: 96 - x_96 = [-1.38037 -5.26003], p_k = [ 0.00124 -0.0014 ], α_k = 0.0625
Iteration: 97 - x_97 = [-1.38029 -5.26012], p_k = [-0.00266 -0.00092], α_k = 0.03125
Iteration: 98 - x_98 = [-1.38037 -5.26015], p_k = [ 0.00102 -0.00119], α_k = 0.0625
Iteration: 99 - x_99 = [-1.38031 -5.26022], p_k = [-0.0022  -0.00079], α_k = 0.03125
Iteration: 100 - x_100 = [-1.38038 -5.26025], p_k = [ 0.00085 -0.00101], α_k = 0.0625
Iteration: 101 - x_101 = [-1.38032 -5.26031], p_k = [-0.00183 -0.00067], α_k = 0.03125
Iteration: 102 - x_102 = [-1.38038 -5.26033], p_k = [ 0.0007  -0.00086], α_k = 0.0625
Iteration: 103 - x_103 = [-1.38034 -5.26039], p_k = [-0.00151 -0.00058], α_k = 0.03125
Iteration: 104 - x_104 = [-1.38039 -5.2604 ], p_k = [ 0.00058 -0.00073], α_k = 0.0625
Iteration: 105 - x_105 = [-1.38035 -5.26045], p_k = [-0.00126 -0.0005 ], α_k = 0.03125
Iteration: 106 - x_106 = [-1.38039 -5.26047], p_k = [ 0.00048 -0.00062], α_k = 0.0625
Iteration: 107 - x_107 = [-1.38036 -5.26051], p_k = [-0.00104 -0.00042], α_k = 0.03125
Iteration: 108 - x_108 = [-1.38039 -5.26052], p_k = [ 0.00039 -0.00053], α_k = 0.0625
Iteration: 109 - x_109 = [-1.38037 -5.26055], p_k = [-0.00086 -0.00036], α_k = 0.03125
Iteration: 110 - x_110 = [-1.38039 -5.26056], p_k = [ 0.00033 -0.00045], α_k = 0.0625
Iteration: 111 - x_111 = [-1.38037 -5.26059], p_k = [-0.00072 -0.00031], α_k = 0.03125
Iteration: 112 - x_112 = [-1.3804 -5.2606], p_k = [ 0.00027 -0.00038], α_k = 0.0625
Iteration: 113 - x_113 = [-1.38038 -5.26062], p_k = [-0.00059 -0.00027], α_k = 0.03125
Iteration: 114 - x_114 = [-1.3804  -5.26063], p_k = [ 0.00022 -0.00032], α_k = 0.0625
Iteration: 115 - x_115 = [-1.38038 -5.26065], p_k = [-0.00049 -0.00023], α_k = 0.03125
Iteration: 116 - x_116 = [-1.3804  -5.26066], p_k = [ 0.00018 -0.00028], α_k = 0.0625
Series diverged.
time: 76.4 ms

We observe that Steepest Descent takes quite a while for iterations before realizing that the function is unoptimizable.

3.

Compute and solve the equation of the linear regression line corresponding to the univariate input-output data \((x, y)\) given by \(\{(−2, 12),(−1, 11),(0, 8),(1, 5),(2, 2),(3, −3)\}\). Plot these points and the computed line in the \((x, y)\)-plane.

Least-Squares / Linear Regression Problem:

(237)\[\begin{align} \underset{\beta}{\text{minimize }} &\frac{1}{2N}\Big(y - X\beta\Big)^2 \\ \end{align}\]

Gradient Vector First-order Optimality Condition:

(238)\[\begin{align} \nabla_\beta\frac{1}{2N}\Big(y - X\beta\Big)^2 &= 0 \\ \frac{1}{N}\Bigg(-X^\top\Big(y - X\beta\Big)\Bigg) &= 0 \\ X^\top X\beta &= X^\top y \\ \hat{\beta} &= (X^\top X)^{-1}X^\top y \\ \end{align}\]

Hessian Second Order Sufficient Condition:

(239)\[\begin{align} &\nabla^2_\beta\frac{1}{2N}\Big(y - X\beta\Big)^2 \\ &\nabla_\beta\frac{1}{N}\Bigg(-X^\top\Big(y - X\beta\Big)\Bigg) \\ &\frac{1}{N}\Bigg(-X^\top y + X^\top X\beta\Big)\Bigg) \\ &\frac{1}{N}X^\top X \\ \end{align}\]

The Hessian is positive semi-definite proof:

For any vector \(z: z \in \mathbb{R}^n\),

(240)\[\begin{align} z X^\top Xz &= {\vert\vert Xz \vert\vert}^2_2 \\ &\geq 0 \blacksquare \end{align}\]

As long as \(X^\top X\) is invertible (by Invertible Matrix Theorem, non-zero determinant, 0 not an eigenvalue), together with Hessian being at least positive semi-definite, Hessian will be positive definite and the stationary point we found from first-order optimality conditions will yield a global minimizer since Hessian is positive definite for any \(\beta\) and function is strictly convex.

X, y = (
    np.array([-2, -1, 0, 1, 2, 3]),
    np.array([12, 11, 8, 5, 2, -3]),
)
X = np.concatenate([np.ones((X.shape[0], 1)), np.expand_dims(X, axis=1)], axis=1)
β_hat = np.linalg.inv(X.T @ X) @ X.T @ y
x = np.linspace(X[:, 1].min(), X[:, 1].max(), 1000)
plt.scatter(X[:, 1], y, label="data points")
plt.plot(
    x,
    np.concatenate([np.ones((x.shape[0], 1)), np.expand_dims(x, axis=1)], axis=1)
    @ β_hat,
    label=f"OLS line: y = {np.round(β_hat[1], 2)}x + {np.round(β_hat[0], 2)}",
)
plt.grid(True)
plt.legend()
plt.title("Fitted Linear Regression OLS solution")
plt.show()
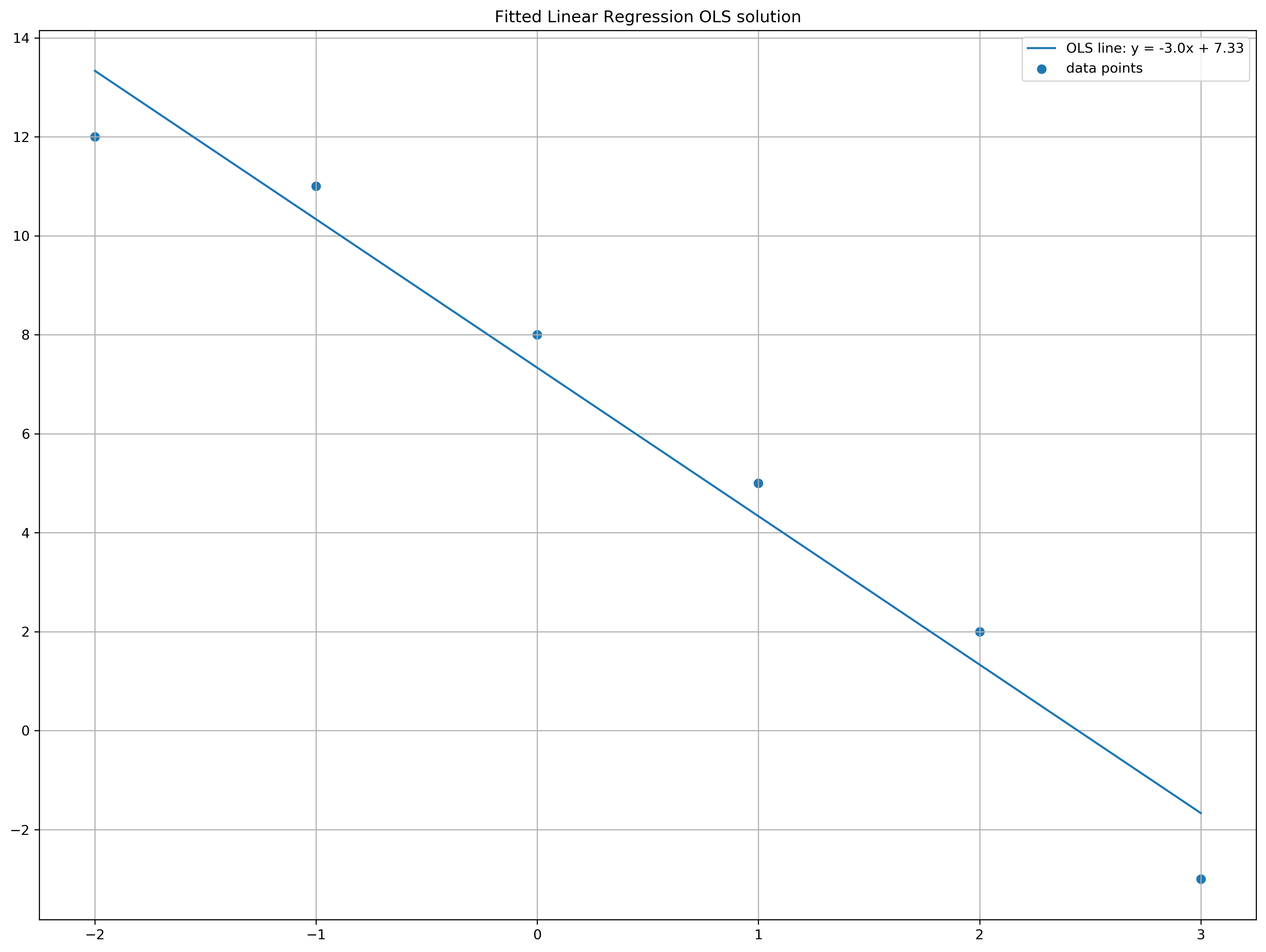
../../_images/hw4_83_0.png 
time: 1.69 s

4.

Suppose that the (univariate) variable \(y\) is known to be a quadratic function of the variable \(x\); that is,

(241)\[\begin{align} y = ax^2 +bx + c, \end{align}\]

where the coefficients \(a, b, c\) are obtained by conducting an experiment in which values \(y_1, \cdots, y_n\) of the variable \(y\) are measured for corresponding values \(x_1, \cdots, x_n\) of the variable \(x\). Find the best least-squares fit of the quadratic polynomial using the data:

(242)\[\begin{align} &\{ (−2, −5),(−1, −1),(0, 4),(1, 7),(2, 6),(3, 5),(4, −1) \}. \end{align}\]

Plot these points and the computed quadratic curve in the \((x, y)\)-plane.

data = [(-2, -5), (-1, -1), (0, 4), (1, 7), (2, 6), (3, 5), (4, -1)]
X, y = np.array(list(zip(*data)))
X = np.concatenate(
    [
        np.ones((X.shape[0], 1)),
        np.expand_dims(X, axis=1),
        np.expand_dims(X ** 2, axis=1),
    ],
    axis=1,
)
β_hat = np.linalg.inv(X.T @ X) @ X.T @ y
x = np.linspace(X[:, 1].min(), X[:, 1].max(), 1000)
plt.scatter(X[:, 1], y, label="data points")
plt.plot(
    x,
    np.concatenate(
        [
            np.ones((x.shape[0], 1)),
            np.expand_dims(x, axis=1),
            np.expand_dims(x ** 2, axis=1),
        ],
        axis=1,
    )
    @ β_hat,
    label=f"OLS line: y = {np.round(β_hat[2], 2)}x^2 + {np.round(β_hat[1], 2)}x + {np.round(β_hat[0], 2)}",
)
plt.grid(True)
plt.legend()
plt.title("Fitted Linear Regression OLS solution with constant, $x$, and $x^2$ terms")
plt.show()
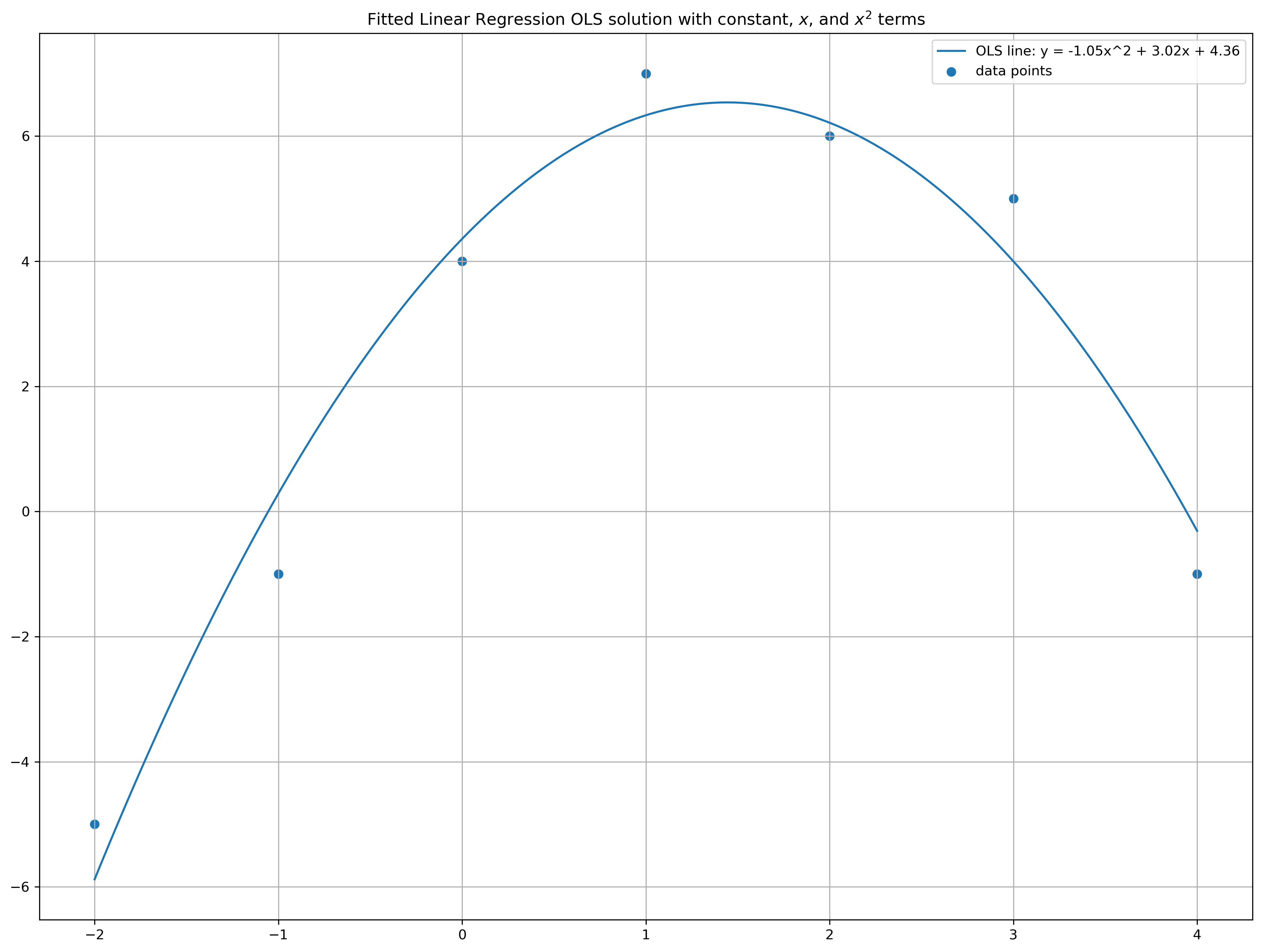
../../_images/hw4_85_0.png 
time: 1.79 s

5

Show that the matrix

(243)\[\begin{align} \begin{bmatrix} x^4 & x^3 & x^2 \\ x^3 & x^2 & x \\ x^2 & x & 1 \\ \end{bmatrix} \end{align}\]

is positive semidefinite but not positive definite for all values of the scalar \(x\).

Proof:

Since \(x\) is a scalar, divide 1st row by \(x^2\), and 2nd row by \(x\):

(244)\[\begin{align} \begin{bmatrix} x^2 & x & 1 \\ x^2 & x & 1 \\ x^2 & x & 1 \\ \end{bmatrix} \end{align}\]

Subtract 1st row from 2nd and last row:

(245)\[\begin{align} \begin{bmatrix} x^2 & x & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \end{align}\]

Any triangular / diagonal matrix’s diagonal entries are its eigenvalues: Hence, our Eigenvalues \(\lambda = x^2, 0, 0\). Since our eigenvalues are \(\geq 0\), but not \(> 0\), we have a positive semidefinite matrix, but not a positive definite matrix. \(\blacksquare\)

HW 3 HW 5